



Next: Fun with Visualizing Modular
Up: The Shafarevich-Tate Group
Previous: Verifying the Full Conjecture
Contents
A major very central conjecture in modern number theory is that
if 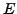 is an elliptic curve over
is an elliptic curve over
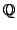 then
then
is finite. This is a theorem when
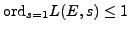 , and is
not known in a single case when
, and is
not known in a single case when
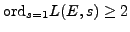 .
Proving finiteness of
.
Proving finiteness of
 for any curve of rank
for any curve of rank 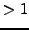 would be a
massively important result that would have huge ramifications.
Much work toward the Birch and Swinnerton-Dyer conjecture (of
Greenberg, Skinner, Urban, Nekovar, etc.) assumes finiteness
of
would be a
massively important result that would have huge ramifications.
Much work toward the Birch and Swinnerton-Dyer conjecture (of
Greenberg, Skinner, Urban, Nekovar, etc.) assumes finiteness
of
 . Note that if
. Note that if
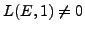 or
or
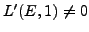 ,
then it is a theorem that
,
then it is a theorem that
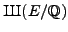 is finite; there
isn't even a single curve with
is finite; there
isn't even a single curve with
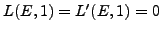 for which
finiteness of
for which
finiteness of
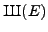 is known.
is known.
As far as I can tell nobody has even the slightest clue how
to prove this. However, we can at least try to do some computations.
Remark 8.8.6 (From Christian Wuthrich.)
Seems doable. I quickly run shark up to p
= 53, it does not take too long. As far as I remember I never
actually checked if shark is optimal when computing the p-adic
L-function.
Remark 8.8.7
In theory one can verify that
![$ {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E)[p] = 0$](img415.png)
for
any
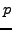
using a
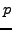
-descent. In practice this does not seem
practical except for
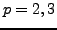
. For
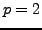
use mwrank
or
simon_two_descent in
SAGE. For
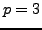
use
three_selmer_rank in
SAGE (this command just
calls MAGMA and runs code of Michael Stoll).
Remark 8.8.8
The work of Cristian Wuthrich and Stein mentioned in
Section
8.8.1 could be used to verify finiteness for many
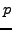
. And Perrin-Riou does exactly this in the supersingular case in
[
PR03]. (In fact, she does much more, in that
she computes
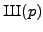
in the whole
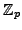
tower. Shark contains now
her computations with a few modifications. - from Christian
Wuthrich.)




Next: Fun with Visualizing Modular
Up: The Shafarevich-Tate Group
Previous: Verifying the Full Conjecture
Contents
William Stein
2006-10-20