


Next: Questions and Comments from
Up: ELLIPTIC CURVES, THE ABC
Previous: Szpiro and ABC
We now state Szpiro's conjecture over a number field.
Let 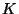 be a number field,
be a number field,
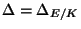 the minimal discriminant
and
the minimal discriminant
and
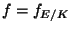 the conductor, and let
the conductor, and let
be the Szpiro ratio.
Conjecture 3.1 (Szpiro)
Given
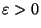
there are only finitely many
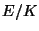
with
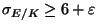
. In particular,
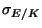
is bounded.
This conjecture is true if one restricts to curves with potential
good reduction everywhere (with ``
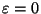 '').
'').
One can also look at modular degrees of coverings of
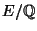 by
by
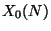 . Any polynomial bound on the modular degree in terms of the
conductor would imply Szpiro's conjecture. It's possible to get
exponential bounds (see work of Stewart and Yu).
. Any polynomial bound on the modular degree in terms of the
conductor would imply Szpiro's conjecture. It's possible to get
exponential bounds (see work of Stewart and Yu).
Theorem 3.2 (Hindry and Silverman (1988), Invent.
93)
There are explicit constants
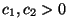
such that for
all number fields
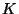
, all elliptic curves
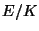
, and
all nontorsion points
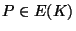
,
we have
In particular, Lang's conjecture is ``as easy as ABC''.
We also get a uniformity result for integral points on curves.
Corollary 3.3
Let
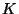
be a number field.
Then there exists
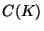
such that if
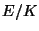
is a ``
minimal''
elliptic curve, then for any finite set of places of
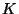
(including the archimedian places)
then we have
In particular, for
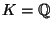
and
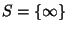
,
the number of integral points on
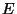
is bounded only in terms of the rank of
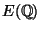
(assuming
that the
's are bounded).



Next: Questions and Comments from
Up: ELLIPTIC CURVES, THE ABC
Previous: Szpiro and ABC
William A Stein
2001-12-20
![]() be a number field,
be a number field,
![]() the minimal discriminant
and
the minimal discriminant
and
![]() the conductor, and let
the conductor, and let
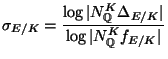
![]() '').
'').
![]() by
by
![]() . Any polynomial bound on the modular degree in terms of the
conductor would imply Szpiro's conjecture. It's possible to get
exponential bounds (see work of Stewart and Yu).
. Any polynomial bound on the modular degree in terms of the
conductor would imply Szpiro's conjecture. It's possible to get
exponential bounds (see work of Stewart and Yu).