


Next: Hindry and Silverman's Paper
Up: ELLIPTIC CURVES, THE ABC
Previous: Motivating Problem
Szpiro's conjecture predated the ABC conjecture, and was made in response
to studying elliptic curves.
Conjecture 2.1 (ABC)
Given
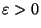
there exists
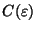
such that
if
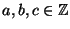
are nonzero and
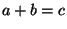
and
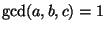
,
then
where
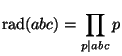
.
Conjecture 2.2 (Szpiro)
Given
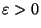
, there exists a constant
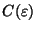
such that
given
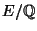
an elliptic curve with minimal discriminant
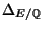
, and conductor
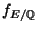
, we have
Conjecture 2.3 (Modified Szpiro)
Given
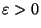
, there exists a constant
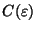
such that
given
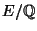
an elliptic curve with invariants
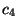
,
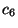
,
and conductor
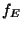
, we have
Fact: The ABC conjecture and the Modified Szpiro conjecture are
equivalent. Also ABC
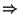 Szpiro
Szpiro
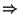 ABC with
exponent of
ABC with
exponent of
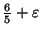 .
.
The connection is through Frey curves. The Frey curve attached to 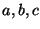 is
is
where 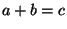 (or something like that), and
(or something like that), and
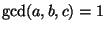 .
For simplicity suppose
.
For simplicity suppose  that
that
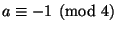 and
and
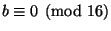 .
Then
.
Then
To see that modified Szpiro implies Szpiro, note that
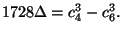 The reason we mention this
implication is because we will apply Szpiro's conjecture in
the original form, not the modified form.
The reason we mention this
implication is because we will apply Szpiro's conjecture in
the original form, not the modified form.
To see that modified Szpiro implies ABC, which is the direction that
we don't need, proceed as follows. If we have that 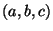 satisfies
satisfies 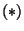 , apply modified Szpiro to the Frey curve
, apply modified Szpiro to the Frey curve
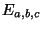 .
.
To see that ABC implies modified Szpiro, proceed as follows.
Fix an elliptic curve
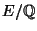 . Construct three integers:
. Construct three integers:
Suppose, for simplicity, that
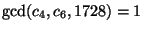 .
Then this really is an ABC triple, and we can apply the ABC conjecture,
and we get that
where
In fact,
.
Then this really is an ABC triple, and we can apply the ABC conjecture,
and we get that
where
In fact,
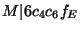 . Then Modified Szpiro follows easily
from this.
. Then Modified Szpiro follows easily
from this.
Fact:
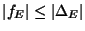 always, which follows from
Ogg's Formula. In fact, the quotient measures the number
of components; more precisely,
always, which follows from
Ogg's Formula. In fact, the quotient measures the number
of components; more precisely,
where 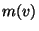 is the number of connected
components of the special fiber of thhe Neron model
of
is the number of connected
components of the special fiber of thhe Neron model
of 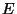 at
at 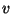 .
(In fact, this is one way to define the conductor, but there
is a more natural definition that comes from Galois theory.)
.
(In fact, this is one way to define the conductor, but there
is a more natural definition that comes from Galois theory.)



Next: Hindry and Silverman's Paper
Up: ELLIPTIC CURVES, THE ABC
Previous: Motivating Problem
William A Stein
2001-12-20
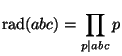 .
.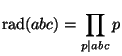 .
.![]() Szpiro
Szpiro
![]() ABC with
exponent of
ABC with
exponent of
![]() .
.
![]() is
is
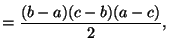
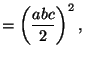
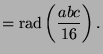
![]() The reason we mention this
implication is because we will apply Szpiro's conjecture in
the original form, not the modified form.
The reason we mention this
implication is because we will apply Szpiro's conjecture in
the original form, not the modified form.
![]() satisfies
satisfies ![]() , apply modified Szpiro to the Frey curve
, apply modified Szpiro to the Frey curve
![]() .
.
![]() . Construct three integers:
. Construct three integers:
![]() always, which follows from
Ogg's Formula. In fact, the quotient measures the number
of components; more precisely,
always, which follows from
Ogg's Formula. In fact, the quotient measures the number
of components; more precisely,