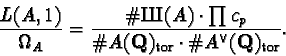Next: The ratio
Up: No Title
Previous: Objectives
My primary objective is to verify the BSD conjecture for
specific modular abelian varieties by using the
rich theory of their arithmetic.
The BSD conjecture asserts that if A is a modular abelian
variety with
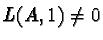 ,
then
,
then
Here
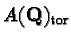 is the group of rational torsion points on A;
the Shafarevich-Tate group
is the group of rational torsion points on A;
the Shafarevich-Tate group
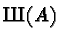 is a measure of the failure
of the local-to-global principle; the Tamagawa numbers cp are the
orders of certain component groups associated to A;
the real number
is a measure of the failure
of the local-to-global principle; the Tamagawa numbers cp are the
orders of certain component groups associated to A;
the real number 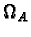 is
the volume of
A(R) with respect to a basis of differentials having
everywhere nonzero good reduction; and
is
the volume of
A(R) with respect to a basis of differentials having
everywhere nonzero good reduction; and 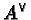 is the dual of A.
is the dual of A.
William A. Stein
1999-12-01
![]() ,
then
,
then