William Stein's homepage



Next: The ratio
Up: Invariants of modular abelian
Previous: Invariants of modular abelian
By [6] we now know
that every elliptic curve over
Q is
a quotient of the curve X0(N) whose complex points
are the isomorphism classes of pairs consisting of a
(generalized) elliptic curve and a cyclic subgroup of order N.
Let J0(N) denote the Jacobian of X0(N); this is an abelian
variety of dimension equal to the genus of X0(N) whose points
correspond to the degree 0 divisor classes on X0(N).
An optimal quotient of J0(N) is a quotient by an abelian subvariety.
Consider an optimal quotient A such that
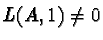 .
By [13],
A(Q) and
.
By [13],
A(Q) and
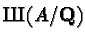 are both finite.
The BSD conjecture asserts that
are both finite.
The BSD conjecture asserts that
Here the Shafarevich-Tate group
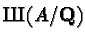 is a measure of the failure
of the local-to-global principle; the Tamagawa numbers cp are the
orders of the component groups of A; the real number
is a measure of the failure
of the local-to-global principle; the Tamagawa numbers cp are the
orders of the component groups of A; the real number 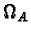 is
the volume of
A(R) with respect to a basis of differentials having
everywhere nonzero good reduction; and
is
the volume of
A(R) with respect to a basis of differentials having
everywhere nonzero good reduction; and 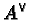 is the dual of A.
My goal is to verify the full
conjecture for many specific abelian varieties on a case-by-case basis.
This is the first step in a program to verify the above
conjecture for an infinite family of quotients of J0(N).
is the dual of A.
My goal is to verify the full
conjecture for many specific abelian varieties on a case-by-case basis.
This is the first step in a program to verify the above
conjecture for an infinite family of quotients of J0(N).



Next: The ratio
Up: Invariants of modular abelian
Previous: Invariants of modular abelian
William A. Stein
1999-12-01
![]() .
By [13],
A(Q) and
.
By [13],
A(Q) and
![]() are both finite.
The BSD conjecture asserts that
are both finite.
The BSD conjecture asserts that