William Stein's homepage

Bibliography

1

A. Agashé, On invisible elements of the Tate-Shafarevich group, C. R. Acad. Sci. Paris Sér. I Math. 328 (1999), no. 5, 369-374.

2

A. Agashé and W.A. Stein, Visibility of Shafarevich-Tate groups of modular abelian varieties, in preparation (1999).

3

E. Artin, Über eine neue Art von L-Reihen, Abh. Math. Sem. Univ. Hamburg 3 (1923), 89-108.

4

B.J. Birch, Elliptic curves over Q: A progress report, 1969 Number Theory Institute (Proc. Sympos. Pure Math., Vol. XX, State Univ. New York, Stony Brook, N.Y., 1969), Amer. Math. Soc., Providence, R.I., 1971, pp. 396-400.

5

S. Bloch and K. Kato, L-functions and Tamagawa numbers of motives, The Grothendieck Festschrift, Vol. I, Birkhäuser Boston, Boston, MA, 1990, pp. 333-400.

6

C. Breuil, B. Conrad, F. Diamond, and R. Taylor, On the modularity of elliptic curves over Q, in preparation.

7

K. Buzzard, M. Dickinson, N. Shepherd-Barron, and R. Taylor, On icosahedral Artin representations, available at http://www.math.harvard.edu/~rtaylor/.

8

K. Buzzard and R. Taylor, Companion forms and weight one forms, Annals of Math. (1999).

9

J.E. Cremona, Algorithms for modular elliptic curves, second ed., Cambridge University Press, Cambridge, 1997.

10

J.E. Cremona and B. Mazur, Visualizing elements in the Shafarevich-Tate group, Proceedings of the Arizona Winter School (1998).

11

N.D. Elkies, Elliptic and modular curves over finite fields and related computational issues, Computational perspectives on number theory (Chicago, IL, 1995), Amer. Math. Soc., Providence, RI, 1998, pp. 21-76.

12

V.A. Kolyvagin, On the structure of Shafarevich-Tate groups, Algebraic geometry (Chicago, IL, 1989), Springer, Berlin, 1991, pp. 94-121.

13

V.A. Kolyvagin and D.Y. Logachev, Finiteness of 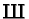$\mbox{\cyr X}$ over totally real fields, Math. USSR Izvestiya 39 (1992), no. 1, 829-853.

14

S. Lang and J. Tate, Principal homogeneous spaces over abelian varieties, Amer. J. Math. 80 (1958), 659-684.

15

B. Mazur, Rational points of abelian varieties with values in towers of number fields, Invent. Math. 18 (1972), 183-266.

16

to3em, Modular curves and the Eisenstein ideal, Inst. Hautes Études Sci. Publ. Math. (1977), no. 47, 33-186 (1978).

17

to3em, Rational isogenies of prime degree (with an appendix by D. Goldfeld), Invent. Math. 44 (1978), no. 2, 129-162.

18

to3em, Visualizing elements of order three in the Shafarevich-Tate group, preprint (1999).

19

L. Merel, Sur la nature non-cyclotomique des points d'ordre fini des courbes elliptiques, preprint (1999).

20

J.-F. Mestre and J. Oesterlé, Courbes de Weil semi-stables de discriminant une puissance m-ième, J. Reine Angew. Math. 400 (1989), 173-184.

21

K.A. Ribet, On modular representations of 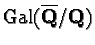${\rm {G}al}(\overline{\bf {Q}}/{\bf {Q}})$ arising from modular forms, Invent. Math. 100 (1990), no. 2, 431-476.

22

to3em, Raising the levels of modular representations, Séminaire de Théorie des Nombres, Paris 1987-88, Birkhäuser Boston, Boston, MA, 1990, pp. 259-271.

23

A.J. Scholl, An introduction to Kato's Euler systems, Galois Representations in Arithmetic Algebraic Geometry, Cambridge University Press, 1998, pp. 379-460.

24

J-P. Serre, Sur les représentations modulaires de degré 2 de 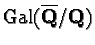${\rm {G}al}(\overline{\bf {Q}}/{\bf {Q}})$, Duke Math. J. 54 (1987), no. 1, 179-230.

25

W.A. Stein, Component groups of optimal quotients of Jacobians, preprint (1999).

26

R. Taylor and A.J. Wiles, Ring-theoretic properties of certain Hecke algebras, Ann. of Math. (2) 141 (1995), no. 3, 553-572.

27

J. Tunnell, Artin's conjecture for representations of octahedral type, Bull. Amer. Math. Soc. (N.S.) 5 (1981), no. 2, 173-175.

28

A.J. Wiles, Modular elliptic curves and Fermat's last theorem, Ann. of Math. (2) 141 (1995), no. 3, 443-551.