Next: Definition of Integral Up: The Definite Integral Previous: The definition of area Contents Index
| Time (seconds) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Speed (mph) | 0 | 5 | 15 | 25 | 40 | 50 | 60 |
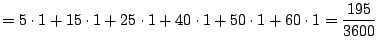 miles
miles
Insight! The formula for the estimate of distance traveled
above looks exactly like an approximation for the area under
the graph of the speed of the car! In fact, if an object
has velocity ![]() at time
at time ![]() , then the net change in position
from time
, then the net change in position
from time ![]() to
to ![]() is
is
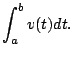
We'll come back to this observation frequently.
William Stein 2006-03-15