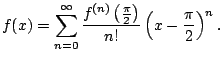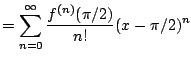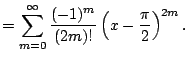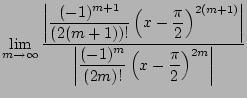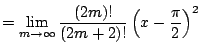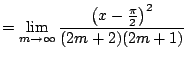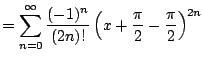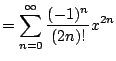Final exam: Wednesday, March 22, 7-10pm in PCYNH 109. Bring ID!
Last Quiz 4: This Friday
Next: 11.10 Taylor and Maclaurin series
Next: 11.12 Applications of Taylor Polynomials
Midterm Letters:
A, 32-38
B, 26-31
C, 20-25
D, 14-19
Mean: 23.4, Standard Deviation: 7.8, High: 38, Low: 6.
|
Example 6.6.1
Suppose we have a degree-
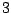
(cubic) polynomial
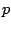
and
we know that
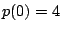
,
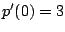
,
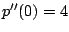
, and
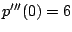
.
Can we determine
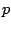
? Answer: Yes!
We have
From what we mentioned above, we have:
Thus
Amazingly, we can use the idea of Example ![[*]](/usr/share/latex2html/icons/crossref.png) to compute power
series expansions of functions. E.g., we will show below that
to compute power
series expansions of functions. E.g., we will show below that
Convergent series are determined by the values
of their derivatives.
Consider a general power series
We have
where for the last equality we use that
Remark 6.6.2
The definition of
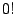
is
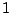
(it's the empty product).
The empty sum is
0 and the empty product is
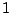
.
Theorem 6.6.3 (Taylor Series
)
If 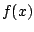 is a function that equals a power series centered
about
is a function that equals a power series centered
about 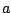 , then that power series expansion is
, then that power series expansion is
Remark 6.6.4
WARNING: There are functions that have all derivatives defined, but do
not equal their Taylor expansion. E.g.,
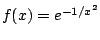
for
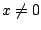
and
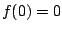
. It's Taylor expansion is the
0 series (which
converges everywhere), but it is not the
0 function.
Definition 6.6.5 (Maclaurin Series)
A
Maclaurin series is just a Taylor series with
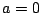
.
I will not use the term ``Maclaurin series'' ever again (it's common
in textbooks).
Example 6.6.6
Find the Taylor series for
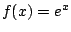
about
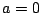
.
We have
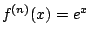
. Thus
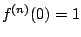
for all
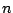
. Hence
What is the radius of convergence?
Use the ratio test:
Thus the radius of convergence is
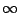
.
Example 6.6.7
Find the Taylor series of
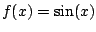
about
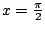
.
6.1 We have
To do this we have to
puzzle out a pattern:
First notice how the signs behave.
For
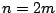
even,
and for
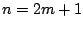
odd,
For
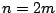
even we have
and for
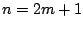
odd we have
Finally,
Next we use the ratio test to compute the radius of convergence.
We have
which converges for each
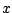
. Hence
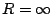
.
Example 6.6.8
Find the Taylor series for
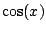
about
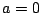
.
We have
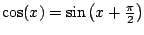
.
Thus from Example
![[*]](/usr/share/latex2html/icons/crossref.png)
(with infinite radius
of convergence) and that the Taylor
expansion is unique, we have
William Stein
2006-03-15
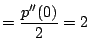
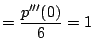
![]() to compute power
series expansions of functions. E.g., we will show below that
to compute power
series expansions of functions. E.g., we will show below that
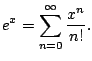
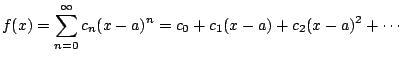
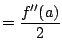
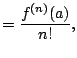
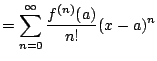
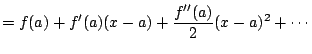
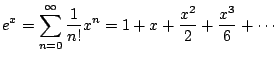
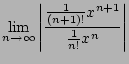
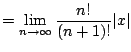
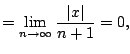 for any fixed
for any fixed