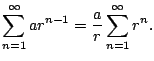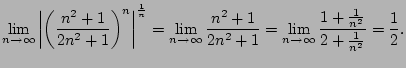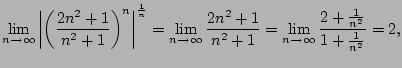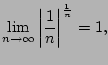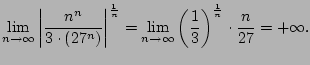The Root Test

Since $e$ and $\ln$ are inverses, we have $x = e^{\ln(x)}$. This implies the very useful fact that

$$x^a = e^{\ln(x^a)} = e^{a\ln(x)}.$$

As a sample application, notice that for any nonzero $c$,

$$\lim_{n\to\infty} c^{\frac{1}{n}} = \lim_{n\to\infty} e^{ \frac{1}{n} \log(c)} = e^0 = 1.$$

Similarly,

$$\lim_{n\to\infty} n^{\frac{1}{n}} = \lim_{n\to\infty} e^{\frac{1}{n} \log(n)} = e^0 = 1,$$

where we've used that $\lim_{n\to\infty} \frac{\log(n)}{n} = 0$, which we could prove using L'Hopital's rule.

Theorem 6.4.10 (Root Test)   Consider the sum $\sum_{n=1}^{\oo } a_n$.

1. If $\lim_{n\to\infty} \vert a_n\vert^{\frac{1}{n}} = L < 1$, then $\sum_{n=1}^{\infty} a_n$ convergest absolutely.
2. If $\lim_{n\to\infty} \vert a_n\vert^{\frac{1}{n}} = L > 1$, then $\sum_{n=1}^{\infty} a_n$ diverges.
3. If $L=1$, then we may conclude nothing from this!

Proof. We apply the comparison test (Theorem 6.4.1). First suppose $\lim_{n\to\infty} \vert a_n\vert^{\frac{1}{n}} = L < 1$. Then there is a $N$ such that for $n\geq N$ we have $\vert a_n\vert^{\frac{1}{n}} < k < 1$. Thus for such $n$ we have $\vert a_n\vert < k^n < 1$. The geometric series $\sum_{i=N}^{\infty} k^i$ converges, so $\sum_{i=N}^{\oo } \vert a_n\vert$ also does, by Theorem 6.4.1. If $\vert a_n\vert^{\frac{1}{n}} > 1$ for $n\geq N$, then we see that $\sum_{i=N}^{\oo } \vert a_n\vert$ diverges by comparing with $\sum_{i=N}^{\infty} 1$. $\qedsymbol$

Example 6.4.11   Let's apply the root test to

$$\sum_{n=1}^{\infty} a r^{n-1} = \frac{a}{r} \sum_{n=1}^{\infty} r^n.$$

We have

$$\lim_{n\to\infty} \vert r^n\vert^{\frac{1}{n}} = \vert r\vert.$$

Thus the root test tells us exactly what we already know about convergence of the geometry series (except when $\vert r\vert=1$).

Example 6.4.12   The sum $\sum_{n=1}^{\infty} \left(\frac{n^2+1}{2n^2+1}\right)^n$ is a candidate for the root test. We have

$$\lim_{n\to \infty} \left\vert\left(\frac{n^2+1}{2n^2+1}\right)^n\... ...} = \lim_{n\to \infty} \frac{1+\frac{1}{n^2}}{2+\frac{1}{n^2}} = \frac{1}{2}.$$

Thus the series converges.

Example 6.4.13   The sum $\sum_{n=1}^{\infty} \left(\frac{2n^2+1}{n^2+1}\right)^n$ is a candidate for the root test. We have

$$\lim_{n\to \infty} \left\vert\left(\frac{2n^2+1}{n^2+1}\right)^n\... ...2+1}{n^2+1} = \lim_{n\to \infty} \frac{2+\frac{1}{n^2}}{1+\frac{1}{n^2}} = 2,$$

hence the series diverges!

Example 6.4.14   Consider $\sum_{n=1}^{\infty} \frac{1}{n}$. We have

$$\lim_{n\to\oo } \left\vert \frac{1}{n} \right\vert^{\frac{1}{n}} = 1,$$

so we conclude nothing!

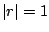
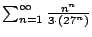
Example 6.4.15   Consider $\sum_{n=1}^{\infty} \frac{n^n}{3\cdot (27^n)}$. To apply the root test, we compute

$$\lim_{n\to\infty} \left\vert \frac{n^n}{3\cdot (27^n)} \right\ver... ...to\infty} \left(\frac{1}{3}\right)^{\frac{1}{n}} \cdot \frac{n}{27} = +\infty.$$

Again, the limit diverges, as in Example 6.4.8.