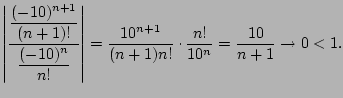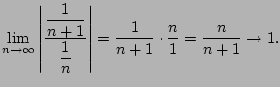Proof.
We will only prove 1.
Assume that we have
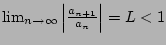
. Let
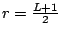
, and notice
that
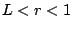
(since
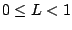
, so
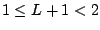
, so
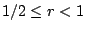
,
and also
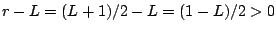
).
Since
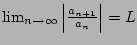 , there is
an
, there is
an 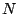 such that for all
such that for all 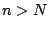 we have
we have
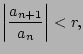
so
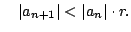
Then we have
Here the common ratio for the second one is
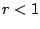
, hence
thus the right-hand series converges, so the left-hand
series converges.

Example 6.4.7
Consider
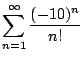
.
The ratio of successive terms is
Thus this series converges
absolutely.
Note, the minus sign is missing above since in the ratio test
we take the limit of the absolute values.
Example 6.4.9
Let's apply the ratio test to
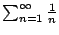
.
We have
This tells us nothing.
If this happens... do something else! E.g., in this case, use the
integral test.
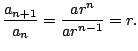
![]() , there is
an
, there is
an ![]() such that for all
such that for all ![]() we have
we have
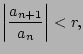 so
so 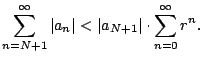
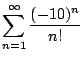 .
The ratio of successive terms is
.
The ratio of successive terms is