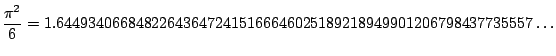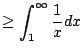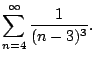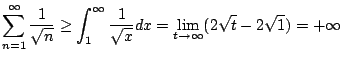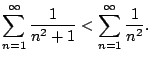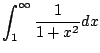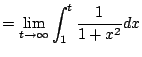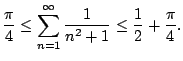Midterm Exam 2: Wednesday March 1 at 7pm in PCYNH 109 (up to last lecture)
Today: §7.3-7.4: Integral and comparison tests
Next: §7.6: Absolute convergence; ratio and root tests
Quiz 4 (last quiz): Friday March 10.
Final exam: Wednesday, March 22, 7-10pm in PCYNH 109.
|
What is
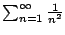 ? What is
? What is
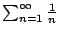 ?
?
Recall that Section 6.2 began by asking for the sum of
several series. We found the first two sums (which were geometric
series) by finding an exact formula for the sum 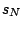 of the first
of the first 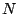 terms. The third series was
terms. The third series was
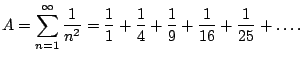 |
(6.1) |
It is difficult to find a nice formula for the sum of the first
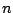 terms of this series (i.e., I don't know how to do it).
terms of this series (i.e., I don't know how to do it).
Remark 6.3.1
Since I'm a number theorist, I can't help but make some further
remarks about sums of the form (
6.3.1).
In general, for any
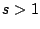
one can consider the sum
The number
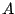
that we are interested in above is thus
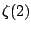
.
The function
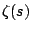
is called the
Riemann zeta function.
There is a natural (but complicated) way of extending
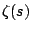
to a
(differentiable) function on all complex numbers with a pole at
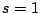
.
The
Riemann Hypothesis asserts that if
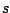
is a complex number
and
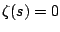
then either
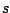
is an even negative integer or
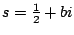
for some real number
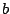
. This is probably
the
most famous unsolved problems in mathematics (e.g., it's one of the
Clay Math Institute million dollar prize problems). Another famous
open problem is to show that
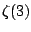
is not a root of any
polynomial with integer coefficients (it is a theorem of
Apeéry that
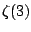
is not a fraction).
The function 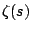 is incredibly important in mathematics
because it governs the properties of prime numbers. The Euler
product representation of
is incredibly important in mathematics
because it governs the properties of prime numbers. The Euler
product representation of 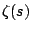 gives a hint as to why this
is the case:
gives a hint as to why this
is the case:
To see that this product equality holds when
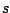
is real
with
Re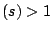
, use Example
6.2.2 with
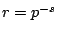
and
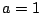
from the
previous lecture. We have
Thus
where the last line uses the distributive law and that integers
factor uniquely as a product of primes.
Finally, Figure 6.3.1 is a graph 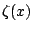 as a
function of a real variable
as a
function of a real variable 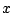 , and Figure 6.3.2 is a graph
of
, and Figure 6.3.2 is a graph
of
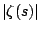 for complex
for complex 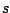 .
.
Figure:
Riemann Zeta Function:
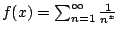
|
|
Figure 6.3.2:
Absolute Value of Riemann Zeta Function
|
|
This section is how to leverage what you've learned so far in this
book to say something about sums that are hard (or even ``impossibly
difficult'') to evaluate exactly. For example, notice (by considering
a graph of a step function) that if
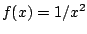 , then for positive
integer
, then for positive
integer 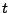 we have
we have
Thus
We conclude that
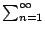 converges, since the sequence
of partial sums is getting bigger and bigger and is always
converges, since the sequence
of partial sums is getting bigger and bigger and is always 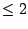 .
And of course we also know something about
.
And of course we also know something about
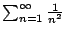 even though we do not know the exact value:
even though we do not know the exact value:
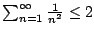 .
Using a computer we find that
The table is consistent with the fact that
.
Using a computer we find that
The table is consistent with the fact that
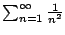 converges to
a number
converges to
a number 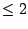 . In fact Euler was the first
to compute
. In fact Euler was the first
to compute
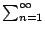 exactly; he
found that the exact value is
There are many proofs of this fact, but they don't
belong in this book; you can find them on the internet,
and are likely to see one if you take more math classes.
exactly; he
found that the exact value is
There are many proofs of this fact, but they don't
belong in this book; you can find them on the internet,
and are likely to see one if you take more math classes.
We next consider the harmonic series
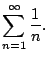 |
(6.2) |
Does it converge? Again by inspecting a graph and viewing
an infinite sum as the area under a step function, we have
Thus the infinite sum (6.3.2) must also diverge.
We formalize the above two examples as a general test for
convergence or divergence of an infinite sum.
The proposition means that you can determine convergence of an
infinite series by determining convergence of a corresponding
integral. Thus you can apply the powerful tools you know
already for integrals to understanding infinite sums.
Also, you can use integration along with computation of
the first few terms of a series to approximate a series
very precisely.
Remark 6.3.3
Sometimes the first few terms of a series are ``funny''
or the series doesn't even start at
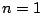
, e.g.,
In this case use (
6.3.3) with any specific
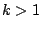
.
Example 6.3.5
Does
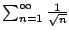 converge?
converge?
No. We have
Example 6.3.6
Does
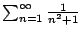 converge?
converge?
Let's apply the comparison test: we have
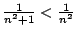
for
every
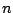
, so
Alternatively, we can use the integral test, which also gives
as a bonus an upper and lower bound on the sum.
Let
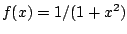
. We have
Thus the sum converges. Moreover, taking
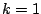
in Theorem
6.3.2
we have
the actual sum is
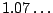
, which is much different than
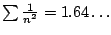
.
We could prove the following proposition using methods similar to those
illustrated in the examples above. Note that this is nicely illustrated
in Figure 6.3.1.
Proposition 6.3.7
The series
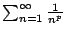 is convergent if
is convergent if 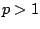 and divergent if
and divergent if 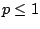 .
.
Subsections
William Stein
2006-03-15
![]() ? What is
? What is
![]() ?
?
![]() of the first
of the first ![]() terms. The third series was
terms. The third series was
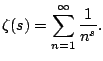
![]() is incredibly important in mathematics
because it governs the properties of prime numbers. The Euler
product representation of
is incredibly important in mathematics
because it governs the properties of prime numbers. The Euler
product representation of ![]() gives a hint as to why this
is the case:
gives a hint as to why this
is the case:
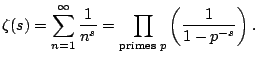
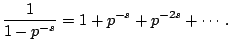
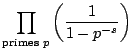
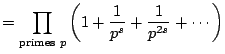
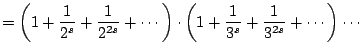
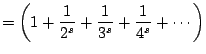
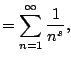
![]() as a
function of a real variable
as a
function of a real variable ![]() , and Figure 6.3.2 is a graph
of
, and Figure 6.3.2 is a graph
of
![]() for complex
for complex ![]() .
.
![]() , then for positive
integer
, then for positive
integer ![]() we have
we have
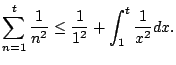
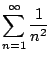
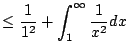
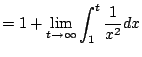
![$\displaystyle = 1 + \lim_{t\to\infty} \left[-\frac{1}{x}\right]_1^t$](img1025.png)
![$\displaystyle = 1 + \lim_{t\to\infty} \left[-\frac{1}{t} + \frac{1}{1} \right] = 2$](img1026.png)