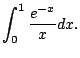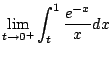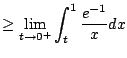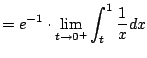In this section we discuss using comparison to determine if an
improper integrals converges or diverges.
Recall that if 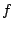 and
and 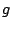 are continuous functions on an
interval
are continuous functions on an
interval ![$ [a,b]$](img17.png) and
and
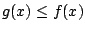 , then
This observation can be incredibly useful
in determining whether or not an improper integral
converges.
, then
This observation can be incredibly useful
in determining whether or not an improper integral
converges.
Not only does this
technique help in determing whether integrals converge, but it also
gives you some information about their values, which is often much
easier to obtain than computing the exact integral.
Proof.
Since
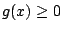
for all
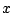
, the function
is a non-decreasing function.
If
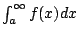
converges to some value
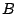
, then
for any
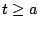
we have
Thus in this case
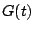
is a non-decreasing function bounded
above, hence the limit
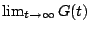
exists.
This proves the first statement.
Likewise, the function
is also a non-decreasing function.
If
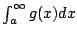
diverges then
the function
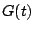
defined above is still non-decreasing and
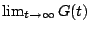
does not exist, so
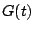
is not bounded. Since
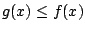
we
have
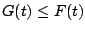
for all
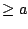
, hence
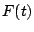
is also unbounded, which proves the second statement.

The theorem is very intuitive if you think about areas under a graph.
``If the bigger integral converges then so does the smaller one, and
if the smaller one diverges so does the bigger ones.''
Example 5.7.9
Does
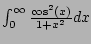
converge? Answer: YES.
Figure:
Graph of
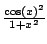 and
and
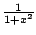
|
|
Since
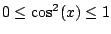 , we really do have
, we really do have
as illustrated in Figure
5.7.5.
Thus
so
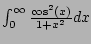
converges.
But why did we use
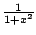 ? It's a guess that turned out
to work. You could have used something else, e.g.,
? It's a guess that turned out
to work. You could have used something else, e.g.,
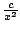 for
some constant
for
some constant 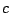 . This is an illustration of how in mathematics
sometimes you have to use your imagination or guess and see what
happens. Don't get anxious--instead, relax, take a deep breath and
explore.
. This is an illustration of how in mathematics
sometimes you have to use your imagination or guess and see what
happens. Don't get anxious--instead, relax, take a deep breath and
explore.
For example, alternatively we could have done the following:
and this works just as well, since
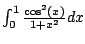
converges (as
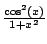
is continuous).
Example 5.7.10
Consider
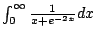
. Does it converge
or diverge?
For large values of
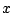
, the term
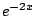
very quickly goes to
0,
so we expect this to diverge, since
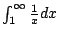
diverges.
For
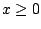
, we have
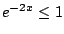
, so
for all
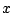
we have
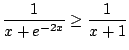
(verify by cross multiplying)

But
Thus
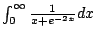
must also diverge.
Note that there is a natural analogue of Theorem 5.7.8
for integrals of functions that ``blow up'' at a point, but
we will not state it formally.
Example 5.7.11
Consider
We have
(Coming up with this comparison might take some work, imagination,
and trial and error.)
We have
thus
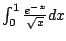
converges, even though
we haven't figured out its value. We just know that it is
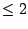
.
(In fact, it is
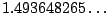
.)
What if we found a function that is bigger than
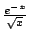 and its integral diverges?? So what! This does
nothing for you. Bzzzt. Try again.
and its integral diverges?? So what! This does
nothing for you. Bzzzt. Try again.
Example 5.7.12
Consider the integral
This is an improper integral since
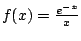
has a pole at
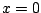
.
Does it converge? NO.
On the interal
![$ [0,1]$](img933.png)
we have
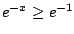
.
Thus
Thus
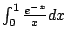
diverges.
William Stein
2006-03-15
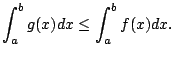
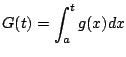
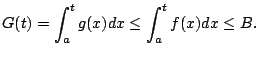
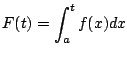
![]() , we really do have
, we really do have
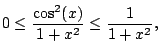
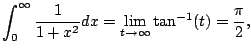
![]() ? It's a guess that turned out
to work. You could have used something else, e.g.,
? It's a guess that turned out
to work. You could have used something else, e.g.,
![]() for
some constant
for
some constant ![]() . This is an illustration of how in mathematics
sometimes you have to use your imagination or guess and see what
happens. Don't get anxious--instead, relax, take a deep breath and
explore.
. This is an illustration of how in mathematics
sometimes you have to use your imagination or guess and see what
happens. Don't get anxious--instead, relax, take a deep breath and
explore.
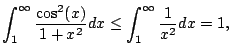
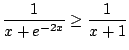 (verify by cross multiplying)
(verify by cross multiplying)![$\displaystyle \int_{1}^{\infty} \frac{1}{x+1} dx
= \lim_{t\to\infty} [\ln(x+1)]_1^{t}
= \infty
$](img923.png)
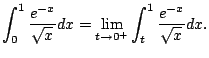
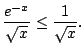
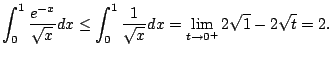
![]() and its integral diverges?? So what! This does
nothing for you. Bzzzt. Try again.
and its integral diverges?? So what! This does
nothing for you. Bzzzt. Try again.