Next: Complex Numbers Up: Areas in Polar Coordinates Previous: Areas in Polar Coordinates Contents Index
Solution: We need the boundaries of integration. Start at
![]() and go to
and go to
![]() . As a check, note that
. As a check, note that
![]() We evaluate
We evaluate
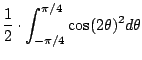 |
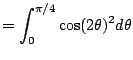 (even function) (even function) |
|
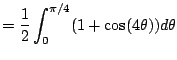 |
||
![$\displaystyle = \frac{1}{2} \left[ \theta + \frac{1}{4}\cdot \sin(4\theta)\right]_{0}^{\pi/4}$](img335.png) |
||
Solution: This is the same as before. It's the difference of two areas.
Figure out the limits, which are where the curves intersect,
i.e., the ![]() such that
such that
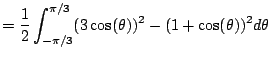 |
||
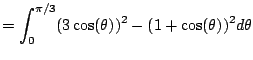 (even function) (even function) |
||
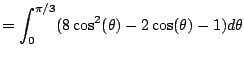 |
||
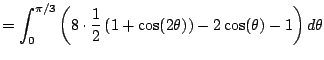 |
||
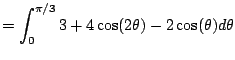 |
||
![$\displaystyle = \Bigl[3\theta + 2 \sin(2\theta) - 2\sin(\theta)\Bigr]_{0}^{\pi/3}$](img354.png) |
||
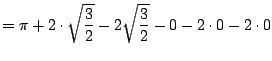 |
||
William Stein 2006-03-15