An odd function is a function 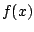 such that
such that
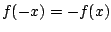 ,
and an even function one for which
,
and an even function one for which
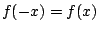 .
If
.
If 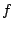 is an odd function, then for any
is an odd function, then for any 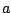 ,
If
,
If 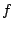 is an even function, then for any
is an even function, then for any 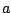 ,
Both statements are clear if we view integrals as computing
the signed area between the graph of
,
Both statements are clear if we view integrals as computing
the signed area between the graph of 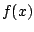 and the
and the 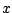 -axis.
-axis.
William Stein
2006-03-15
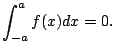
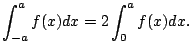
![$\displaystyle \int_{-1}^1 x^2 dx = 2 \int_{0}^1 x^2 dx = 2\left[\frac{1}{3} x^3\right]_{0}^1 = \frac{2}{3}.
$](img172.png)