Next: The Substitution Rule for Up: Substitution and Symmetry Previous: Substitution and Symmetry Contents Index
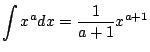 if $a&ne#neq;-1$
if $a&ne#neq;-1$Just as with the power rule, many other rules and results that you already know yield techniques for integration. In general integration is potentially much trickier than differentiation, because it is often not obvious which technique to use, or even how to use it. Integration is a more exciting than differentiation!
Recall the chain rule, which asserts that
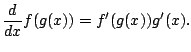
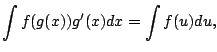
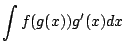 |
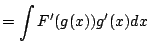 |
|
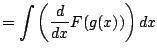 |
||
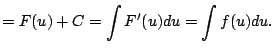 |
If ![]() then
then
![]() , and the substitution rule simply
says if you let
, and the substitution rule simply
says if you let ![]() formally in the integral everywhere, what you
naturally would hope to be true based on the notation actually is
true. The substitution rule illustrates how the notation Leibniz
invented for Calculus is incredibly brilliant. It is said that
Leibniz would often spend days just trying to find the right notation
for a concept. He succeeded.
formally in the integral everywhere, what you
naturally would hope to be true based on the notation actually is
true. The substitution rule illustrates how the notation Leibniz
invented for Calculus is incredibly brilliant. It is said that
Leibniz would often spend days just trying to find the right notation
for a concept. He succeeded.
As with all of Calculus, the best way to start to get your head around a new concept is to see severally clearly worked out examples. (And the best way to actually be able to use the new idea is to do lots of problems yourself!) In this section we present examples that illustrate how to apply the substituion rule to compute indefinite integrals.
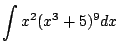
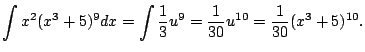
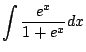
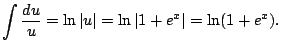
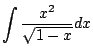
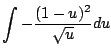 |
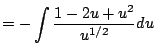 |
|
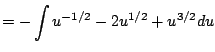 |
||
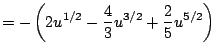 |
||
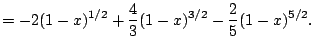 |
William Stein 2006-03-15