


Next: Skipping Next Monday
Up: Remarks
Previous: Projective Space
Consider a cubic curve of the form
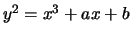 and
assume that
and
assume that 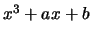 has distinct roots.
Then the set
is the graph of the real points on an elliptic curve. Given two
solutions
has distinct roots.
Then the set
is the graph of the real points on an elliptic curve. Given two
solutions 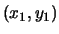 and
and
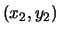 , there is a formula for
a third solution
, there is a formula for
a third solution 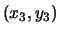 . It has the marvelous properties that
. It has the marvelous properties that
- If
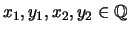 then
then
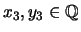 .
.
- The composition law turns the set
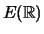 into a GROUP.
into a GROUP.
The composition law is described in the text both algebraically and
geometrically, but a complete proof that it has property 2 above is
not given. I'm not sure what we'll do about this. My advice is that
you would be best served to just believe this on faith at this point.
When you learn ``algebraic geometry'' later in your career, you'll learn
a beautiful and conceptually satisfying definition of the group law.
William A Stein
2003-02-11