William Stein
Date: Math 124 ![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001
(1 point) Why do you think that quadratic reciprocity is
so cool?
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .
.
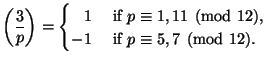
![]() for any
for any ![]() .
.
![]() is a prime, then
there is a primitive root modulo
is a prime, then
there is a primitive root modulo ![]() .
.
![]() is cyclic to give a direct proof
that
is cyclic to give a direct proof
that
![]() when
when
![]() . [Hint: There is an
. [Hint: There is an
![]() of
order
of
order ![]() . Show that
. Show that
![]() .]
.]
![]() , show directly that
, show directly that
![]() by the method of
Exercise 5. [Hint: Let
by the method of
Exercise 5. [Hint: Let
![]() be an element of
order
be an element of
order ![]() . Show that
. Show that
![]() , etc.]
, etc.]
![]() is
is
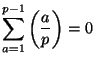 ?
?
![]() such that
such that ![]() is a primitive root
modulo
is a primitive root
modulo ![]() is asymptotic to
is asymptotic to ![]() where
where ![]() is the number of
primes
is the number of
primes ![]() and
and ![]() is a fixed constant called Artin's constant.
Using a computer, make an educated guess as to what
is a fixed constant called Artin's constant.
Using a computer, make an educated guess as to what ![]() should be, to
a few decimal places of accuracy. Explain your reasoning. (Note:
Don't try to prove that your guess is correct.)
should be, to
a few decimal places of accuracy. Explain your reasoning. (Note:
Don't try to prove that your guess is correct.)
![]()
![]()
![]()
Next: About this document ...
William A Stein
2001-12-10