Elliptic Curve Analogues of Diffie-Hellman
The Diffie-Hellman
key exchange from Section 3.1
works well on an elliptic curve
with no serious modification.
Michael and Nikita
agree on a secret key as follows:
- Michael and Nikita agree on a prime
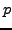 , an
elliptic curve
, an
elliptic curve 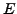 over
over
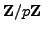 , and a point
, and a point
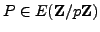 .
.
- Michael secretly chooses a random
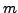 and sends
and sends 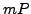 .
.
- Nikita secretly chooses a random
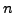 and sends
and sends 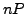 .
.
- The secret key is
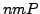 , which both Michael and
Nikita can compute.
, which both Michael and
Nikita can compute.
Presumably, an adversary can not compute
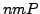 without solving the discrete logarithm
problem
(see Problem 3.1.2 and Section 6.4.3 below)
in
without solving the discrete logarithm
problem
(see Problem 3.1.2 and Section 6.4.3 below)
in
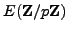 . For well-chosen
. For well-chosen 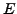 ,
, 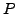 , and
, and 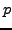 experience suggests
that the discrete logarithm problem
in
experience suggests
that the discrete logarithm problem
in
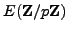 is much more difficult than the discrete
logarithm problem in
is much more difficult than the discrete
logarithm problem in
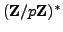 (see Section 6.4.3 for more on the elliptic
curve discrete log problem).
(see Section 6.4.3 for more on the elliptic
curve discrete log problem).
William
2007-06-01