The Diffie-Hellman Key Exchange
As night darkens Nikita's cell, she reflects on what has happened.
Upon realizing that she mis-remembered how the system works, she phones
Michael and they do the following:
- Together Michael and Nikita choose a 200-digit integer
 that
is likely to be prime (see Section 2.4), and
choose a number
that
is likely to be prime (see Section 2.4), and
choose a number 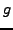 with
with 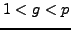 .
.
- Nikita secretly chooses an integer
 .
.
- Michael secretly chooses an integer
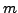 .
.
- Nikita computes
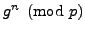 on her handheld computer and tells
Michael the resulting number over the phone.
on her handheld computer and tells
Michael the resulting number over the phone.
- Michael tells Nikita
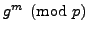 .
.
- The shared secret key is then
which both Nikita and Michael can compute.
Here is a simplified example that illustrates what they did, that
involves only relatively simple arithmetic.
Subsections
William
2007-06-01