Computing Primitive Roots

Theorem 2.5.8 does not suggest an efficient algorithm for finding primitive roots. To actually find a primitive root mod $p$ in practice, we try $a=2$ , then $a=3$ , etc., until we find an $a$ that has order $p-1$ . Computing the order of an element of $(\mathbb{Z}/p\mathbb{Z}{})^*$ requires factoring $p-1$ , which we do not know how to do quickly in general, so finding a primitive root modulo $p$ for large $p$ seems to be a difficult problem.

Algorithm 2.5 (Primitive Root)   Given a prime $p$ this algorithm computes the smallest positive integer $a$ that generates $(\mathbb{Z}/p\mathbb{Z}{})^*$ .

1. [$p=2$ ?] If $p=2$ output $1$ and terminate. Otherwise set $a=2$ .
2. [Prime Divisors] Compute the prime divisors $p_1, \ldots, p_r$ of $p-1$ .
3. [Generator?] If for every $p_i$ , we have $a^{(p-1)/p_i} \not\equiv 1\pmod{p}$ , then $a$ is a generator of $(\mathbb{Z}/p\mathbb{Z}{})^*$ , so output $a$ and terminate.
4. [Try next] Set $a=a+1$ and go to step 3.

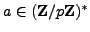
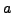
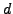
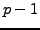
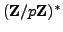
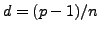
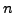
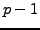
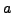
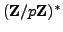
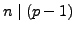
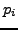
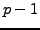
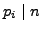
Proof. Let $a\in (\mathbb{Z}/p\mathbb{Z}{})^*$ . The order of $a$ is a divisor $d$ of the order $p-1$ of the group $(\mathbb{Z}/p\mathbb{Z}{})^*$ . Write $d =(p-1)/n$ , for some divisor $n$ of $p-1$ . If $a$ is not a generator of $(\mathbb{Z}/p\mathbb{Z}{})^*$ , then since $n\mid (p-1)$ , there is a prime divisor $p_i$ of $p-1$ such that $p_i\mid n$ . Then

$$a^{(p-1)/p_i} = (a^{(p-1)/n})^{n/p_i} \equiv 1\pmod{p}.$$

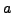
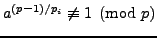
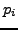
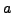
Conversely, if $a$ is a generator, then $a^{(p-1)/p_i} \not\equiv 1\pmod{p}$ for any $p_i$ . Thus the algorithm terminates with step 3 if and only if the $a$ under consideration is a primitive root. By Theorem 2.5.8 there is at least one primitive root, so the algorithm terminates. $\qedsymbol$