Next: The Complex -series Up: The BSD Rank Conjecture Previous: Statement of the BSD Contents Index

Next we show that given the rank ![]() , the
full group
, the
full group ![]() is computable. The issue is that
what we did above might have only computed a subgroup
of finite index. The argument below follows
[Cre97, §3.5] closely.
is computable. The issue is that
what we did above might have only computed a subgroup
of finite index. The argument below follows
[Cre97, §3.5] closely.
The naive height ![]() of a point
of a point
![]() is
is
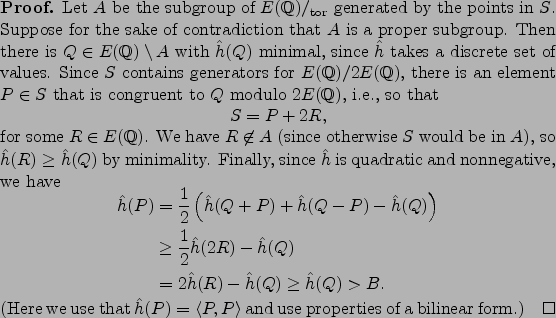

William 2007-05-25