Statement of the BSD Rank Conjecture

An excellent reference for this section is Andrew Wiles's Clay Math Institute paper [Wil00]. The reader is also strongly encouraged to look Birch's original paper [Bir71] to get a better sense of the excitement surrounding this conjecture, as exemplified in the following quote:

``I want to describe some computations undertaken by myself and Swinnerton-Dyer on EDSAC by which we have calculated the zeta-functions of certain elliptic curves. As a result of these computations we have found an analogue for an elliptic curve of the Tamagawa number of an algebraic group; and conjectures (due to ourselves, due to Tate, and due to others) have proliferated.''

An elliptic curve $E$ over a field $K$ is the projective closure of the zero locus of a nonsingular affine curve

$$y^2 + a_1 xy + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6,$$ (1.1.1)

where $a_1,a_2,a_3,a_4,a_6\in K$. There is a simple algebraic condition on the $a_i$ that ensures that (1.1.1) defines a nonsingular curve (see, e.g., [Sil92]).

An elliptic curve $E$ has genus $1$, and the set of points on $E$ has a natural structure of abelian group, with identity element the one extra projective point at $\infty$. Again, there are simple algebraic formulas that, given two points $P$ and $Q$ on an elliptic curve, produce a third point $P+Q$ on the elliptic curve. Moreover, if $P$ and $Q$ both have coordinates in $K$, then so does $P+Q$. The Mordell-Weil group

$$E(K) = \{\text{ points on $E$ with coordinates in $K$ }\}$$

of $E$ over $K$ plays a central role in this book.

In the 1920s, Mordell proved that if $K=\mathbb{Q}$, then $E(\mathbb{Q})$ is finitely generated, and soon after Weil proved that $E(K)$ is finitely generated for any number field $K$, so

$$E(K) \approx \mathbb{Z}^r \oplus T,$$ (1.1.2)

where $T$ is a finite group. Perhaps the chief invariant of an elliptic curve $E$ over a number field $K$ is the rank, which is the number $r$ in (1.1.2).

Fix an elliptic curve $E$ over $\mathbb{Q}$. For all but finitely many prime numbers $p$, the equation (1.1.1) reduces modulo $p$ to define an elliptic curve over the finite field $\mathbb{F}_p$. The primes that must be excluded are exactly the primes that divide the discriminant $\Delta$ of (1.1.1).

As above, the set of points $E(\mathbb{F}_p)$ is an abelian group. This group is finite, because it is contained in the set $\P^2(\mathbb{F}_p)$ of rational points in the projective plane. Moreover, since it is the set of points on a (genus 1) curve, a theorem of Hasse implies that

$$\vert p+1 - \char93 E(\mathbb{F}_p) \vert \leq 2\sqrt{p}.$$

The error terms

$$a_p = p+1 - \char93 E(\mathbb{F}_p)$$

play a central role in almost everything in this book. We next gather together the error terms into a single ``generating function'':

$$\tilde{L}(E,s) = \prod_{p\nmid \Delta} \left( \frac{1}{1 - a_p p^{-s} + p^{1-2s}}\right).$$

The function $\tilde{L}(E,s)$ defines a complex analytic function on some right half plane $\mbox{\rm Re}(s)>\frac{3}{2}$.

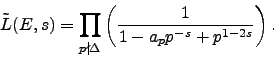
A deep theorem of Wiles et al. [Wil95,BCDT01], which many consider the crowning achievement of 1990s number theory, implies that $\tilde{L}(E,s)$ can be analytically continued to an analytic function on all $\mathbb{C}$. This implies that $\tilde{L}(E,s)$ has a Taylor series expansion about $s=1$:

$$\tilde{L}(E,s) = c_0 + c_1 (s-1) + c_2 (s-1)^2 + \cdots$$

Define the analytic rank $r_{{\rm an}}$ of $E$ to be the order of vanishing of $\tilde{L}(E,s)$ as $s=1$, so

$$\tilde{L}(E,s) = c_{r_{{\rm an}}} (s-1)^{r_{{\rm an}}} + \cdots.$$

The definitions of the analytic and Mordell-Weil ranks could not be more different - one is completely analytic and the other is purely algebraic.

Conjecture 1.1 (Birch and Swinnerton-Dyer Rank Conjecture)   Let $E$ be an elliptic curve over $\mathbb{Q}$. Then the algebraic and analytic ranks of $E$ are the same.

This problem is extremely difficult. The conjecture was made in the 1960s, and hundreds of people have thought about it for over 4 decades. The work of Wiles et al. on modularity in late 1999, combined with earlier work of Gross, Zagier, and Kolyvagin, and many others proves the following partial result toward the conjecture.

Theorem 1.2   Suppose $E$ is an elliptic curve over $\mathbb{Q}$ and that $r_{{\rm an}} \leq 1$. Then the algebraic and analytic ranks of $E$ are the same.

In 2000, Conjecture 1.1 was declared a million dollar millenium prize problem by the Clay Mathematics Institute, which motivated even more work, conferences, etc., on the conjecture. Since then, to the best of my knowledge, not a single new result directly about Conjecture 1.1 has been proved. The class of curves for which we know the conjecture is still the set of curves over $\mathbb{Q}$ with $r_{{\rm an}} \leq 1$, along with a finite set of individual curves on which further computer calculations have been performed (by Cremona, Watkins, myself, and others).

``A new idea is needed.''

- Nick Katz on BSD, at a 2001 Arizona Winter School

And another quote from Bertolini-Darmon (2001):

``The following question stands as the ultimate challenge concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over $\mathbb{Q}$: Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where  $\ord _{s=1} L(E,s) > 1$.''