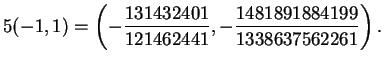Next: About this document ...
Up: Lecture 26: The Elliptic
Previous: An Example Over a
Venerable Problem: Find an algorithm that, given
an elliptic curve 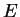 over
over
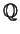 , outputs a complete description
of the set of rational points
, outputs a complete description
of the set of rational points
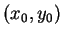 on
on 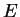 .
.
This problem is difficult. In fact, so far it has stumped everyone!
There is a conjectural algorithm, but nobody has succeeded in proving
that it is really an algorithm, in the sense that it terminates for
any input curve 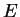 . Several of your profs at Harvard, including
Barry Mazur, myself, and Christophe Cornut (who will teach Math 129
next semester) have spent, or might spend, a huge chunk of
their life thinking about this problem.
. Several of your profs at Harvard, including
Barry Mazur, myself, and Christophe Cornut (who will teach Math 129
next semester) have spent, or might spend, a huge chunk of
their life thinking about this problem.
How could one possible ``describe'' the group
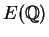 , since it can be
infinite? In 1923, Mordell proved that there is
always a reasonable way to describe
, since it can be
infinite? In 1923, Mordell proved that there is
always a reasonable way to describe
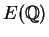 .
.
Theorem 5.1 (Mordell)
The group
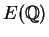
is finitely generated.
This means that there are points
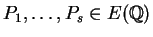 such that every element of
such that every element of
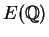 is of the form
is of the form
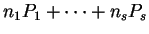 for some
for some
 . I will not prove Mordell's theorem in
this course, but see §1.3 of [Kato et al.].
. I will not prove Mordell's theorem in
this course, but see §1.3 of [Kato et al.].
Example 5.2
Consider the elliptic curve
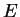
given by
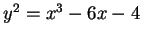
.
Then
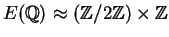
with generators
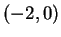
and
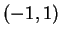
. We have
Trying finding that point without knowing about the group law!



Next: About this document ...
Up: Lecture 26: The Elliptic
Previous: An Example Over a
William A Stein
2001-11-16
![]() . Several of your profs at Harvard, including
Barry Mazur, myself, and Christophe Cornut (who will teach Math 129
next semester) have spent, or might spend, a huge chunk of
their life thinking about this problem.
. Several of your profs at Harvard, including
Barry Mazur, myself, and Christophe Cornut (who will teach Math 129
next semester) have spent, or might spend, a huge chunk of
their life thinking about this problem.
![]() , since it can be
infinite? In 1923, Mordell proved that there is
always a reasonable way to describe
, since it can be
infinite? In 1923, Mordell proved that there is
always a reasonable way to describe
![]() .
.