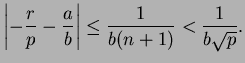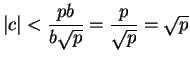Next: Computing and
Up: Sums of Two Squares
Previous: Sums of Two Squares
The main goal of today's lecture is to prove the following theorem.
Theorem 1.1
A number
is a sum of two squares if and only if all prime factors
of
of the form
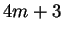
have even exponent in the prime factorization
of
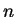
.
Before tackling a proof, we consider a few examples.
Example 1.2
-
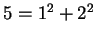 .
.
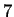 is not a sum of two squares.
is not a sum of two squares.
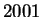 is divisible by
is divisible by 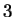 because
because 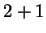 is, but not by
is, but not by 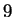 since
since 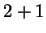 is not, so
is not, so 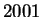 is not a sum of two squares.
is not a sum of two squares.
-
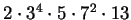 is a sum of two squares.
is a sum of two squares.
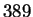 is a sum of two squares, since
is a sum of two squares, since
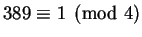 and
and 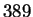 is prime.
is prime.
-
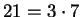 is not a sum of two squares even though
is not a sum of two squares even though
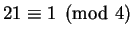 .
.
In preparation for the proof of Theorem 1.1, we recall a
result that emerged when we analyzed how partial convergents
of a continued fraction converge.
Lemma 1.3
If
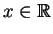
and
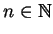
, then there is a fraction
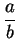
in lowest terms such that
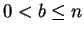
and
Proof.
Let
![$ [a_0,a_1,\ldots]$](img26.png)
be the continued fraction expansion of
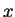
.
As we saw in the proof of Theorem 2.3 in Lecture 18, for each
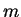
Since
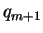
is always at least
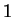
bigger than
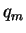
and
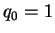
,
either there exists an
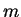
such that
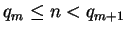
, or the
continued fraction expansion of
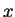
is finite and
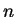
is larger
than the denominator of the rational number
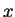
. In the first
case,
so
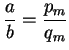
satisfies the conclusion of
the lemma. In the second case, just let
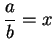
.

Definition 1.4
A representation
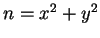
is
primitive if
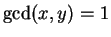
.
Lemma 1.5
If
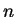
is divisible by a prime
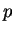
of the form
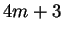
, then
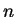
has no primitive representations.
Proof.
If
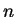
has a primitive representation,
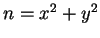
, then
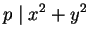
and
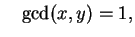
so
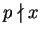
and
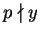
. Thus
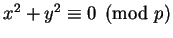
so, since
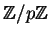
is a field we can divide by
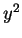
and see that
Thus the quadratic residue symbol
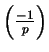
equals
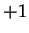
.
However,

Proof.
[Proof of Theorem
1.1]
Suppose that
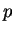
is of the form
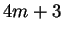
, that
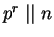
(exactly
divides) with
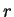
odd, and that
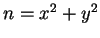
. Letting
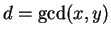
,
we have
with
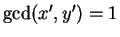
and
Because 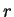 is odd,
is odd, 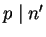 , so Lemma 1.5
implies that
, so Lemma 1.5
implies that
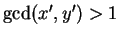 , a contradiction.
, a contradiction.
 Write
Write
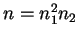 where
where 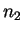 has no prime factors of the
form
has no prime factors of the
form 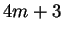 . It suffices to show that
. It suffices to show that 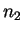 is a sum of two
squares. Also note that
is a sum of two
squares. Also note that
so a product of two numbers that are sums of two squares is also
a sum of two squares.
1Also, the prime
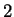
is a sum of two squares.
It thus suffices to show that if
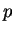
is a prime of the form
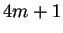
, then
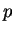
is a sum of two squares.
Since
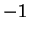
is a square modulo
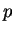
; i.e., there exists
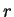
such
that
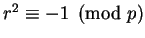
. Taking
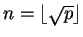
in Lemma
1.3 we see that there are integers
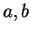
such that
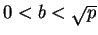
and
If we write
then
and
But
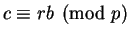
, so
Thus
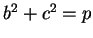
.




Next: Computing and
Up: Sums of Two Squares
Previous: Sums of Two Squares
William A Stein
2001-10-31
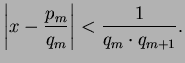
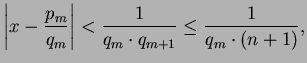
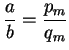 satisfies the conclusion of
the lemma. In the second case, just let
satisfies the conclusion of
the lemma. In the second case, just let
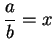 .
.
![]()
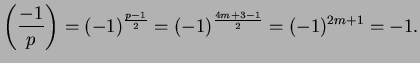
![]() is odd,
is odd, ![]() , so Lemma 1.5
implies that
, so Lemma 1.5
implies that
![]() , a contradiction.
, a contradiction.
![]() Write
Write
![]() where
where ![]() has no prime factors of the
form
has no prime factors of the
form ![]() . It suffices to show that
. It suffices to show that ![]() is a sum of two
squares. Also note that
is a sum of two
squares. Also note that