We study
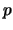
-divisibility of discriminant of Hecke algebras associated
to spaces of cusp forms of prime level. By considering cusp forms of
weight bigger than

, we are are led to make a conjecture about
indexes of Hecke algebras in their normalization which, if true,
implies that there are no mod
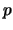
congruences between
non-conjugate newforms in

.