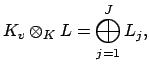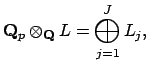Much of this chapter is preparation for what we will do later
when we will prove that if 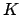 is complete with respect to a valuation
(and locally compact) and
is complete with respect to a valuation
(and locally compact) and 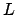 is a finite extension of
is a finite extension of 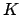 , then there
is a unique valuation on
, then there
is a unique valuation on 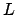 that extends the valuation on
that extends the valuation on 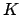 .
Also, if
.
Also, if 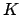 is a number field,
is a number field,
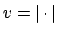 is a valuation on
is a valuation on 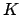 ,
,
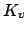 is the completion of
is the completion of 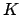 with respect to
with respect to 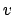 , and
, and 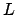 is a
finite extension of
is a
finite extension of 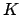 , we'll prove that
where the
, we'll prove that
where the 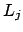 are the completions of
are the completions of 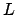 with respect to the
equivalence classes of extensions of
with respect to the
equivalence classes of extensions of 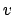 to
to 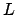 . In particular,
if
. In particular,
if 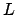 is a number field defined by a root of
is a number field defined by a root of
![$ f(x)\in\mathbf{Q}[x]$](img271.png) , then
where the
, then
where the 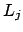 correspond to the irreducible factors of
the polynomial
correspond to the irreducible factors of
the polynomial
![$ f(x) \in \mathbf{Q}_p[x]$](img2070.png) (hence the extensions of
(hence the extensions of
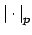 correspond to irreducible factors of
correspond to irreducible factors of 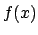 over
over
![$ \mathbf{Q}_p[x]$](img2071.png) ).
).
In preparation for this clean view of the local nature of number
fields, we will prove that the norms on a finite-dimensional
vector space over a complete field are all equivalent. We will also
explicitly construct tensor products of fields and deduce some of
their properties.
Subsections
William Stein
2004-05-06