The following examples are meant to convince you that learning
algebraic number theory now will be an excellent investment of your
time. If an example below seems vague to you, it is safe to
ignore it.
- Integer factorization using the number field sieve. The
number field sieve is the asymptotically fastest known algorithm for
factoring general large integers (that don't have too special of a
form). Recently, in December 2003, the number field sieve was used to
factor the RSA-576 $10000 challenge:
(The
 indicates that the newline should be removed, not that
there are missing digits.)
For more information on the NFS, see
the paper by Lenstra et al. on the Math 129
web page.
indicates that the newline should be removed, not that
there are missing digits.)
For more information on the NFS, see
the paper by Lenstra et al. on the Math 129
web page.
- Primality test: Agrawal and his students Saxena and Kayal from
India recently (2002) found the first ever deterministic
polynomial-time (in the number of digits) primality test. There
methods involve arithmetic in quotients of
![$ (\mathbf{Z}/n\mathbf{Z})[x]$](img16.png) , which are
best understood in the context of algebraic number theory. For
example, Lenstra, Bernstein, and others have done that and improved
the algorithm significantly.
, which are
best understood in the context of algebraic number theory. For
example, Lenstra, Bernstein, and others have done that and improved
the algorithm significantly.
- Deeper point of view on questions in number theory:
- Pell's Equation (
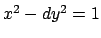 )
)
 Units in real quadratic fields
Units in real quadratic fields
 Unit groups in number fields
Unit groups in number fields
- Diophantine Equations
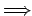 For which
For which 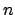 does
does
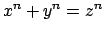 have a
nontrivial solution in
have a
nontrivial solution in
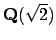 ?
?
- Integer Factorization
 Factorization of ideals
Factorization of ideals
- Riemann Hypothesis
 Generalized Riemann Hypothesis
Generalized Riemann Hypothesis
- Deeper proof of Gauss's quadratic reciprocity law in terms of arithmetic
of cyclotomic fields
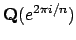 , which leads to class field theory.
, which leads to class field theory.
- Wiles's proof of Fermat's Last Theorem, i.e.,
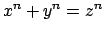 has no nontrivial integer solutions, uses methods from
algebraic number theory extensively (in addition to many other deep
techniques). Attempts to prove Fermat's Last Theorem long ago were
hugely influential in the development of algebraic number theory
(by Dedekind, Kummer, Kronecker, et al.).
has no nontrivial integer solutions, uses methods from
algebraic number theory extensively (in addition to many other deep
techniques). Attempts to prove Fermat's Last Theorem long ago were
hugely influential in the development of algebraic number theory
(by Dedekind, Kummer, Kronecker, et al.).
- Arithmetic geometry: This is a huge field that studies
solutions to polynomial equations that lie in arithmetically
interesting rings, such as the integers or number fields. A famous
major triumph of arithmetic geometry is Faltings's proof of Mordell's
Conjecture.
For example, Theorem 2.3.1 implies that for any 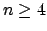 and any number field
and any number field 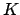 , there are only finitely many solutions
in
, there are only finitely many solutions
in 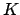 to
to 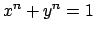 . A famous open problem in arithmetic geometry
is the Birch and Swinnerton-Dyer conjecture, which gives a deep
conjectural criterion for exactly when
. A famous open problem in arithmetic geometry
is the Birch and Swinnerton-Dyer conjecture, which gives a deep
conjectural criterion for exactly when 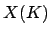 should be infinite when
should be infinite when
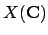 is a torus.
is a torus.
William Stein
2004-05-06
