These are some of the main topics that are discussed in this book:
- Rings of integers of number fields
- Unique factorization of ideals in Dedekind domains
- Structure of the group of units of the ring of integers
- Finiteness of the group of equivalence classes
of ideals of the ring of integers (the ``class group'')
- Decomposition and inertia groups, Frobenius elements
- Ramification
- Discriminant and different
- Quadratic and biquadratic fields
- Cyclotomic fields (and applications)
- How to use a computer to compute with many of the above
objects (both algorithms and actual use of PARI and ).
- Valuations on fields
- Completions (
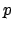 -adic fields)
-adic fields)
- Adeles and Ideles
Note that we will not do anything nontrivial with zeta functions or
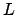 -functions. This is to keep the prerequisites to algebra, and so
we will have more time to discuss algorithmic questions. Depending on
time and your inclination, I may also talk about integer
factorization, primality testing, or complex multiplication elliptic
curves (which are closely related to quadratic imaginary fields).
-functions. This is to keep the prerequisites to algebra, and so
we will have more time to discuss algorithmic questions. Depending on
time and your inclination, I may also talk about integer
factorization, primality testing, or complex multiplication elliptic
curves (which are closely related to quadratic imaginary fields).
William Stein
2004-05-06