First, we write the continued fraction of 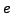 in a slightly different
form. Instead of
in a slightly different
form. Instead of
![$ [2,1,2,1,1,4,\ldots],$](img1798.png) we can start the sequence of
coefficients
we can start the sequence of
coefficients
to make the pattern the same throughout. (Everywhere else in
this chapter we assume that the partial quotients 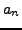 for
for 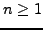 are positive, but temporarily relax that
condition here and allow
are positive, but temporarily relax that
condition here and allow 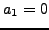 .) The numerators and
denominators of the convergents given by this new sequence satisfy a
simple recurrence. Using
.) The numerators and
denominators of the convergents given by this new sequence satisfy a
simple recurrence. Using 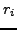 as a stand-in for
as a stand-in for 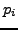 or
or 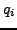 , we
have
, we
have
Our first goal is to collapse these three recurrences into one
recurrence that only makes mention of 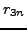 ,
, 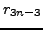 , and
, and
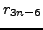 . We have
. We have
This same method of simplification also shows us that
To get rid of 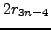 in the first equation, we make the
substitutions
in the first equation, we make the
substitutions
Substituting for 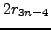 and then
and then 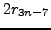 , we finally have the
needed collapsed recurrence,
, we finally have the
needed collapsed recurrence,
William
2007-06-01
![]() ,
, ![]() , and
, and
![]() . We have
. We have