3..
- This problem concerns encoding phrases
using numbers using the encoding of Section 3.2.2.
What is the longest that an arbitrary sequence of letters (no spaces)
can be if it must fit in a number that is less than
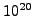 ?
?
- Suppose Michael creates an RSA cryptosystem with a very large
modulus
 for which the factorization of
for which the factorization of  cannot be found
in a reasonable amount of time. Suppose that Nikita sends
messages to Michael by representing each alphabetic character
as an integer between 0
and
cannot be found
in a reasonable amount of time. Suppose that Nikita sends
messages to Michael by representing each alphabetic character
as an integer between 0
and 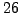 (
(A corresponds
to 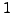 ,
, B to 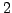 , etc., and a space
, etc., and a space to 0
),
then encrypts each number separately
using Michael's RSA cryptosystem. Is this method secure?
Explain your answer.
-
For any
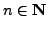 , let
, let 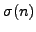 be the
sum of the divisors of
be the
sum of the divisors of  ; for example,
; for example,
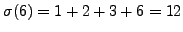 and
and
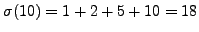 .
Suppose that
.
Suppose that 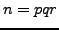 with
with  ,
, 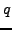 , and
, and 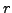 distinct primes. Devise
an ``efficient'' algorithm that given
distinct primes. Devise
an ``efficient'' algorithm that given  ,
,
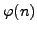 and
and
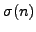 , computes the factorization of
, computes the factorization of  . For example, if
. For example, if
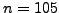 , then
, then 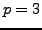 ,
, 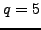 , and
, and 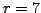 , so the input to the algorithm
would be
, so the input to the algorithm
would be
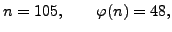
and
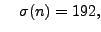
and the output would be 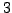 ,
, 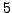 , and
, and 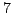 .
.
- You and Nikita wish to agree on a secret key using
the Diffie-Hellman key exchange. Nikita announces that
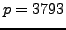 and
and
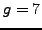 . Nikita secretly chooses a number
. Nikita secretly chooses a number 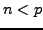 and tells you
that
and tells you
that
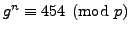 . You choose the random number
. You choose the random number
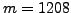 . What is the secret key?
. What is the secret key?
- You see Michael and Nikita agree on a secret
key using the Diffie-Hellman key exchange. Michael and Nikita
choose
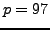 and
and 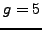 . Nikita chooses a random number
. Nikita chooses a random number  and
tells Michael that
and
tells Michael that
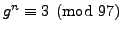 , and Michael chooses a
random number
, and Michael chooses a
random number 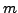 and tells Nikita that
and tells Nikita that
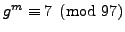 . Brute
force crack their code: What is the secret key that Nikita and
Michael agree upon? What is
. Brute
force crack their code: What is the secret key that Nikita and
Michael agree upon? What is  ? What is
? What is 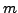 ?
?
-
In this problem, you will ``crack'' an RSA cryptosystem.
What is the secret decoding number
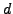 for the RSA
cryptosystem with public key
for the RSA
cryptosystem with public key
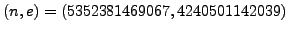 ?
?
- Nikita creates an RSA cryptosystem with public key
In the following two problems, show the steps you take to factor  .
(Don't simply factor
.
(Don't simply factor  directly using a computer.)
directly using a computer.)
- Somehow you discover that
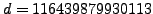 . Show how to use the
probabilistic algorithm of Section 3.3.3 to
use
. Show how to use the
probabilistic algorithm of Section 3.3.3 to
use 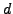 to factor
to factor  .
.
- In part (a) you found that the factors
 and
and 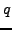 of
of  are very close.
Show how to use the Fermat factorization
method of Section 3.3.2 to factor
are very close.
Show how to use the Fermat factorization
method of Section 3.3.2 to factor  .
.
William
2007-06-01