Factoring $n$ Given $\varphi (n)$

Suppose $n=pq$ . Given $\varphi (n)$ , it is very easy to compute $p$ and $q$ . We have

$$\varphi (n) = (p-1)(q-1) = pq-(p+q)+1,$$

so we know both $pq=n$ and $p+q = n+1 - \varphi (n)$ . Thus we know the polynomial

$$x^2 - (p+q)x + pq = (x-p)(x-q)$$

whose roots are $p$ and $q$ . These roots can be found using the quadratic formula.

Example 3.3   The number $n=pq=31615577110997599711$ is a product of two primes, and $\varphi (n)= 31615577098574867424$ . We have

$$f = x^2 - (n+1-\varphi (n))x + n$$

$$= x^2 - 12422732288x + 31615577110997599711$$

$$= (x-3572144239)(x-8850588049),$$

where the factorization step is easily accomplished using the quadratic formula:

$$\frac{-b +\sqrt{b^2 - 4ac}}{2a}$$

$$\qquad= \frac{ 12422732288 + \sqrt{12422732288^2 - 4\cdot 31615577110997599711}}{2}$$

$$\qquad= 8850588049.$$

We conclude that $n = 3572144239\cdot 8850588049$ .

SAGE Example 3.3   The following SAGE function factors $n=pq$ given $n$ and $\varphi (n)$ .

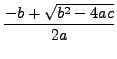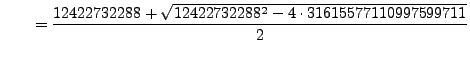sage: def crack_rsa(n, phi_n):
...    R.<x> = PolynomialRing(QQ)
...    f = x^2 - (n+1 -phi_n)*x + n
...    return [b for b, _ in f.roots()]
sage: crack_rsa(31615577110997599711, 31615577098574867424)
[8850588049, 3572144239]