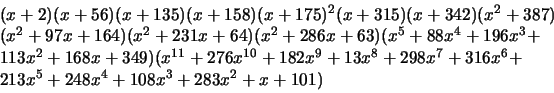Motivation and Applications

Let $p$ be a prime and suppose that $\Gamma=\Gamma_0(p)$ or $\Gamma_1(p)$. The quantity $d_k(\Gamma)$ is of interest because it measures mod $p$ congruences between eigenforms in $S_k(\Gamma)$.

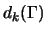
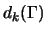
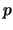
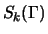
Proposition 3.1   Suppose that $d_k(\Gamma)$ is finite. Then the discriminant valuation $d_k(\Gamma)$ is nonzero if and only if there is a mod-$p$ congruence between two Hecke eigenforms in $S_k(\Gamma)$ (note that the two congruent eigenforms might be Galois conjugate).

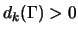
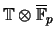
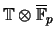
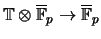
Proof. It follows from Proposition 2.2 that $d_k(\Gamma)>0$ if and only if $\mathbb{T}\otimes \overline{\mathbb{F}}_p$ is not separable. The Artinian ring $\mathbb{T}\otimes \overline{\mathbb{F}}_p$ is not separable if and only if the number of ring homomorphisms $\mathbb{T}\otimes \overline{\mathbb{F}}_p\rightarrow \overline{\mathbb{F}}_p$ is less than

$$\dim_{\overline{\mathbb{F}}_p} \mathbb{T}\otimes \overline{\mathbb{F}}_p= \dim_\mathbb{C}S_k(\Gamma).$$

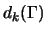
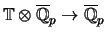
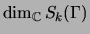
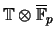
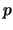
Since $d_k(\Gamma)$ is finite, the number of ring homomorphisms $\mathbb{T}\otimes \overline{\mathbb{Q}}_p\rightarrow \overline{\mathbb{Q}}_p$ equals $\dim_\mathbb{C}S_k(\Gamma)$. Using the standard bijection between congruences and normalized eigenforms, we see that $\mathbb{T}\otimes \overline{\mathbb{F}}_p$ is not separable if and only if there is a mod-$p$ congruence between two eigenforms. $\qedsymbol$

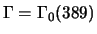
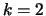
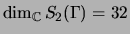
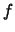
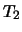
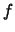
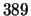
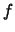
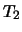
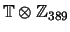
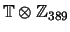
Example 3.2   If $\Gamma=\Gamma_0(389)$ and $k=2$, then $\dim_\mathbb{C}S_2(\Gamma) = 32$. Let $f$ be the characteristic polynomial of $T_2$. One can check that $f$ is square free and $389$ exactly divides the discriminant of $f$, so $T_2$ generated $\mathbb{T}\otimes \mathbb{Z}_{389}$ as a ring. 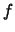(If it generated a subring of $\mathbb{T}\otimes \mathbb{Z}_{389}$ of finite index, then the discriminant of $f$ would be divisible by $389^2$.)

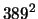
Modulo 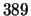$389$ the polynomial 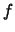$f$ is congruent to

$$\begin{array}{l} (x+2)(x+56)(x+135)(x+158)(x+175)^2(x+315)(x... ...\\ 213x^5 + 248x^4 + 108x^3 + 283x^2 + x + 101) \end{array}$$

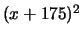
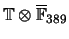
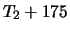
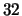
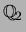
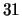
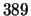
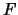
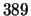
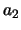
The factor $(x+175)^2$ indicates that $\mathbb{T}\otimes \overline{\mathbb{F}}_{389}$ is not separable since the image of $T_2+175$ is nilpotent (its square is 0). There are $32$ eigenforms over  $\mathbb{Q}_2$ but only $31$ mod-$389$ eigenforms, so there must be a congruence. Let $F$ be the $389$-adic newform whose $a_2$ term is a root of

$$x^2 + (-39 + 190\cdot 389 + 96\cdot 389^2 +\cdots) x + (-106 + 43\cdot 389 + 19\cdot 389^2 + \cdots).$$

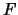
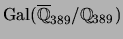
Then the congruence is between $F$ and its $\Gal(\overline{\mathbb{Q}}_{389}/\mathbb{Q}_{389})$-conjugate.

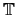
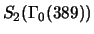
Example 3.3   The discriminant of the Hecke algebra $\mathbb{T}$ associated to $S_2(\Gamma_0(389))$ is

$$2^{53} \!\cdot\! 3^{4} \!\cdot\! 5^{6} \!\cdot\! 31^{2} \!\cdot\!... ...ot\! 389 \!\cdot\! 3881 \!\cdot\! 215517113148241 \!\cdot\! 477439237737571441$$

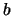
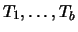
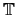
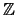
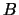
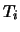
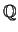
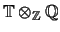
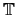
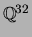
I computed this using the following algorithm, which was suggested by Hendrik Lenstra. Using the Sturm bound I found a $b$ such that $T_1,\ldots,T_b$ generate $\mathbb{T}$ as a $\mathbb{Z}$-module. I then found a subset $B$ of the $T_i$ that form a $\mathbb{Q}$-basis for $\mathbb{T}\otimes _\mathbb{Z}\mathbb{Q}$. 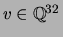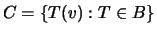Next, viewing $\mathbb{T}$ as a ring of matrices acting on $\mathbb{Q}^{32}$, I found a random vector $v\in\mathbb{Q}^{32}$ such that the set of vectors $C=\{T(v) : T \in B\}$ is linearly independent. 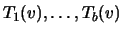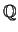Then I wrote each of $T_1(v),\ldots, T_b(v)$ as $\mathbb{Q}$-linear combinations of the elements of $C$. 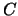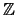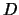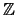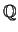Next I found a $\mathbb{Z}$-basis $D$ for the $\mathbb{Z}$-span of these $\mathbb{Q}$-linear combinations of elements of $C$. 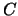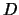Tracing everything back, I find the trace pairing on the elements of $D$, and deduce the discriminant by computing the determinant of the trace pairing matrix. 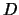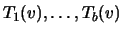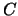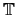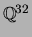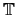The most difficult step is computing $D$ from $T_1(v),\ldots, T_b(v)$ expressed in terms of $C$, and this explains why we embed $\mathbb{T}$ in $\mathbb{Q}^{32}$ instead of viewing the elements of $\mathbb{T}$ as vectors in $\mathbb{Q}^{32^2}$. 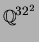This whole computation takes one second on an Athlon 2000 processor.