Definition 2.1 (Discriminant)
Let
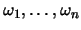
is a
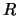
-basis
for
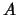
. Then the
discriminant of
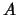
, denoted
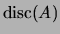
,
is the determinant of the
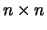
matrix
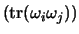
, which is well defined
modulo squares of units in
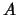
.
Proposition 2.2
Suppose
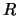
is a field. Then
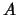
has discriminant 0 if and only
if
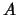
is separable over
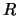
, i.e., for every extension
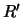
of
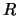
, the ring
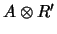
contains no nilpotents.