The Birch and Swinnerton-Dyer Conjecture (Monday)

1. (15 minutes) Congruent number problem; connected to elliptic curves; we need to understand when elliptic curves have points on them.
2. (15 minutes) Daily crashing of the SAGE Notebook - some improvements I made over the weekend: computing E.points() for $E$ an elliptic curve modulo $p$ is now very fast; the Notebook interface is generally more robust and much easier to interrupt; foo?? gives source code even for functions you enter or in cong.sage if you do attach cong.sage; can write, e.g., plot(..., hue=...) instead of plot(..., rgbcolor=hue(...)). So please, right now, try hard to ``crash'' your personal SAGE Notebook, i.e., get it in an unresponsive state. Don't worry, I can easily restart all of them.
3. The Conjecture. The Birch and Swinnerton-Dyer conjecture was made in the 1960s based on numerical computations carried out on EDSAC:

   Let $n$ be a positive square-free integer. This means that no perfect square divides $n$ . Let $E_n$ be the elliptic curve

   $$E_n: \quad y^2 = x^3 - n^2x.$$
   If $n$ is odd, let $N = 32n^2$ , and if $n$ is even, let $N=16n^2$ . The number $N$ is called the conductor of $E_n$ .

   For any prime $p\nmid 2n$ , let

   $$a_p = p + 1 - \char93 E_n(\mathbb{F}_p),$$
   where $\char93 E_n(\mathbb{F}_p)$ is the number of points on the elliptic curve $E_n$ viewed modulo $p$ . If $p\mid 2n$ , let $a_p = 0$ . If $m, r$ are coprime integers, let $a_{mr} = a_m a_r$ . If $p\nmid 2n$ let $a_{p^r} = a_{p^{r-1}} a_p - p a_{p^{r-2}}$ , and if $p\mid 2n$ let $a_{p^r} = 0$ . Finally, let
   $$L(E_n,1) = \begin{cases} 0 & \text{if $n\equiv 5,6,7\pmod{8}$} ... ...infty} \frac{a_k}{k} \cdot e^{-2\pi k/\sqrt{N}} & \text{otherwise}. \end{cases}$$
   Conjecture 5.1 (Birch and Swinnerton-Dyer)  
   
   

   We have $L(E_n,1)=0$ if and only if $E_n(\mathbb{Q})$ is infinite.
   (Stated in a special cases.)

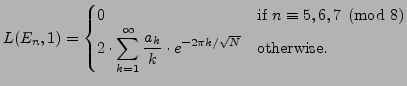
   This is a major open problem in number theory. If I don't solve this problem, I hope one of you does!

   Proof. [Heuristic ``Proof''] (This is a fake ``proof''.) If $E_n(\mathbb{Q})$ is infinite then the numbers $\char93 E_n(\mathbb{F}_p)$ will tend to be big, since you get lots of elements of $E_n(\mathbb{F}_p)$ by reducing the elements of $E_n(\mathbb{Q})$ modulo $p$ . Thus $a_p = p+1 - \char93 E_n(\mathbb{F}_p)$ will tend to be small. One can prove that $L(E_n,1)\geq 0$ , so if the $a_p$ are small, that will ``cause'' the sum that defines $L(E_n,1)$ to be small, i.e., 0 . Conversely if $L(E_n,1)=0$ , then the $E_n(\mathbb{F}_p)$ are big, and the points have to come from somewhere so $E_n(\mathbb{Q})$ is big. $\qedsymbol$
   Theorem 5.2 (Kolyvagin et al.)   If $E_n(\mathbb{Q})$ is infinite then $L(E_n,1)=0$ .
   This is one direction in the conjecture, and the proof is very very difficult. Put another way, this theorem says that if $L(E_n,1)\neq 0$ , then $E_n(\mathbb{Q})$ is finite.

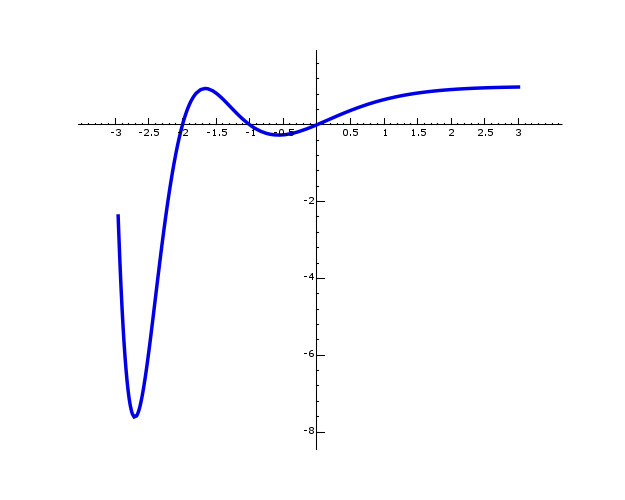
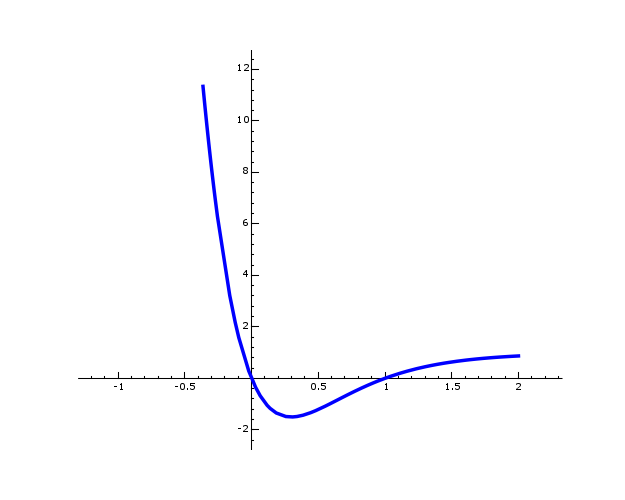
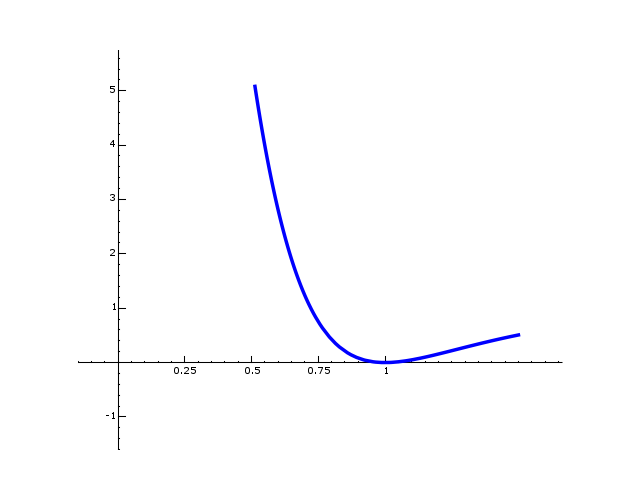
   As the notation suggests, $L(E_n,1)$ is the value of a function at $1$ . I will not define the general function, but here are some plots of $L(E_n,s)$ for various $n$ :

   $n=1$ $n=6$

   $n=34$ $n=4199$

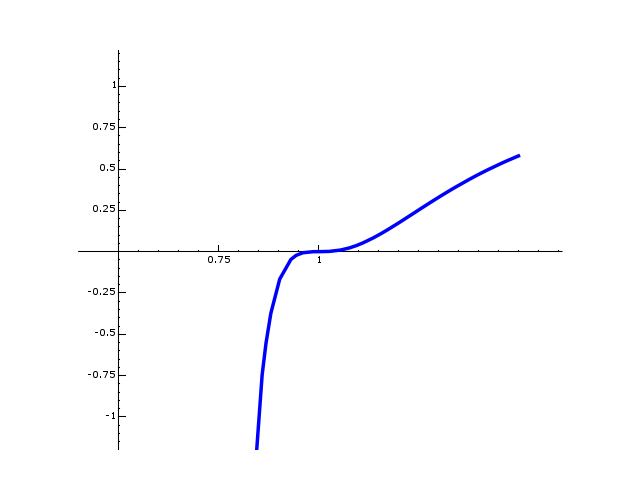
   I made them using code like

   E = EllipticCurve([-6^2,0])
   L = E.Lseries_dokchitser()
   P = plot(L,0.5,1.5, plot_points=50, plot_division=50, 
           rgbcolor=(0,0,1), thickness=2)
   

4. Participants - do the following for $n=1$ and $n=34$ :
   1. Write down $E_n$ .
   2. Find the conductor $N$ of $E_n$ .
   3. Compute (by hand/with computer) $a_1, a_2, a_3, a_4$ , and $a_5$ . Check your answer with SAGE (use E.an(m) to compute $a_m$ ). The point here is to spend some time understanding the definition of $a_m$ .
   4. Compute the first $5$ terms in the sum that defines $L(E_n,1)$ .

      (You should find that for $n=34$ we have $L(E_{34},1)=0$ , whereas for $n=1$ we have $L(E_{1},1)\neq 0$ .)

      sage: E = EllipticCurve([-1^2,0])
      sage: E.Lseries(1)
      0.65551438857302990
      
      sage: E = EllipticCurve([-34^2,0])
      sage: E.Lseries(1)
      -0.0000000000000000...  (the nonzeros at the end are just errors/noise)
      

   5. The following SAGE program can be used to compute the sum that defines $L(E_n,1)$ using any number of terms.

      def L(n, prec):
         E = EllipticCurve([-n^2,0])
         v = E.anlist(prec)
         N = E.conductor()
         sqrtN = sqrt(N)
         lval = 2*sum(v[n]/n*exp(-2*pi*n/sqrtN) for n in range(1,prec))
         return lval
      

      Note: This function is in cong.sage. Just type attach cong.sage if you haven't already and it will magically be available. Then you can enter L? for help and L?? for source code.

5. Participants - Prove using SAGE calculations and the BSD conjecture that none of $1,2,3,4$ are congruent numbers.
6. Participants - Try to find patterns, any at all, in the numbers
   $$p+1-\char93 E_n(\mathbb{F}_p)$$
   for the congruent number curves $y^2 = x^3 - n^2 x$ . E.g., fix $n=1$ and compute these numbers for primes up to some bound:

   E = EllipticCurve([-1,0])
   for p in primes(2,100):
       print p, E.ap(p)
   

• COMPUTATION:
  • This SAGE code draws the plot below. Try different curves, ranges of primes, etc.

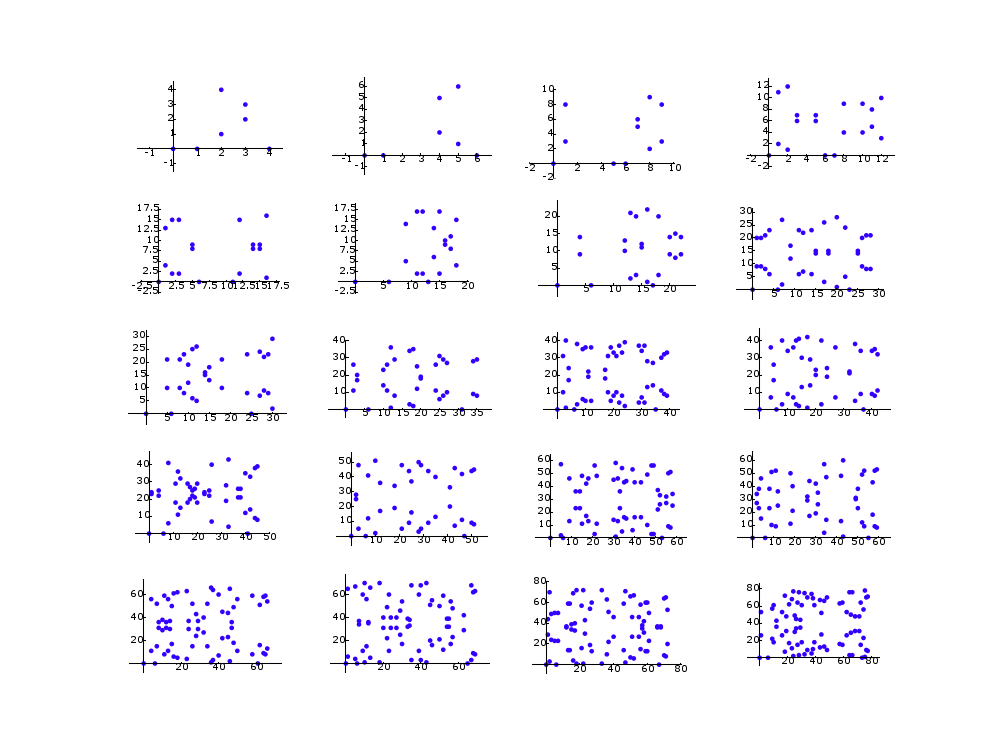
    n = 6
    def pl(p):
        return plot(EllipticCurve(GF(p),[-n^2,0]), rgbcolor=hue(0.7))
    
    P = [pl(p) for p in primes(5,100) if n%p != 0]
    Q = [[P[4*i+j] for j in range(4)] for i in range(len(P)/4)]
    show(graphics_array(Q))
    # show(graphics_array(Q), axes=False)   # if you don't want axes
    

    

  • Make a table of values $L(E_n,1)$ for each integer $n< 50$ . How does this compare to the table of congruent numbers $n< 50$ . [Here's how to approximately compute $L(E,1)$ in SAGE:]

  • In this problem $n$ always denotes a squarefree positive integer $n$ (i.e., no perfect squares divide $n$ ).
    1. If $n\equiv 5,6,7\pmod{8}$ then does the Birch and Swinnerton-Dyer conjecture imply that $n$ is a congruent number?
    2. Are there any integers $n \equiv 3\pmod{8}$ with $n$ a congruent number?

       EllipticCurve([-1,0]).Lseries(1)
       

• THEORY:
  • What is the relationship between the $a_p$ for $E_1$ and $E_6$ ? Make a conjecture based on numerical evidence. Note: you can compute $a_p$ using E.ap(p), e.g.,

    E = EllipticCurve([-1,0])
    for p in primes(10):
        print p, E.ap(p)
    

    Can you say anything about the relation between the $a_p$ for $E_1$ and for $E_n$ for general $n$ ?

• RESEARCH:
  • Find Andrew Wiles's paper on the Birch and Swinnerton-Dyer conjecture at the Clay Math Institute web site http://www.claymath.org/millennium/ and read as much of it as you can. One of their pages says:

    ``Mathematicians have always been fascinated by the problem of describing all solutions in whole numbers $x,y,z$ to algebraic equations like

    $$x^2 + y^2 = z^2.$$

    Euclid gave the complete solution for that equation, but for more complicated equations this becomes extremely difficult. Indeed, in 1970 Yu. V. Matiyasevich showed that Hilbert's tenth problem is unsolvable, i.e., there is no general method for determining when such equations have a solution in whole numbers. But in special cases one can hope to say something. When the solutions are the points of an abelian variety, the Birch and Swinnerton-Dyer conjecture asserts that the size of the group of rational points is related to the behavior of an associated zeta function $L(s)$ near the point $s=1$ . In particular this amazing conjecture asserts that if $L(1)$ is equal to 0 , then there are an infinite number of rational points (solutions), and conversely, if $L(1)$ is not equal to 0, then there is only a finite number of such points.''

  • Noam Elkies web page http://www.math.harvard.edu/~ elkies/compnt.htmlhas the most extensive data I've seen about congruent numbers. Check it out!

  • EDSAC - search for information online about the EDSAC computer.