Next: Bibliography Up: current Previous: Proof of Theorem 3.10
Let ![]() be a normalised rational newform for
be a normalised rational newform for
![]() . Let
. Let
![]() be its period lattice; that is, the lattice of periods of
be its period lattice; that is, the lattice of periods of
![]() over
over
![]() .
.
We know that
![]() is an elliptic curve
is an elliptic curve ![]() defined
over
defined
over ![]() and of conductor
and of conductor ![]() . This is the optimal quotient of
. This is the optimal quotient of
![]() associated to
associated to ![]() . Our goal is two-fold: to identify
. Our goal is two-fold: to identify ![]() (by giving an explicit Weierstrass model for it with integer
coeffients); and to show that the associated Manin constant for
(by giving an explicit Weierstrass model for it with integer
coeffients); and to show that the associated Manin constant for ![]() is
is ![]() . In this section we will give an algorithm for this; our
algorithm applies equally to optimal quotients of
. In this section we will give an algorithm for this; our
algorithm applies equally to optimal quotients of ![]() .
.
As input to our algorithm, we have the following data:
So ![]() is isomorphic over
is isomorphic over ![]() to
to ![]() for a unique
for a unique
![]() .
.
The justification for this uses the full force of the modularity of
elliptic curves defined over ![]() : we have computed a full set of
newforms
: we have computed a full set of
newforms ![]() at level
at level ![]() , and the same number of isogeny classes of
elliptic curves, and the theory tells us that there is a bijection
between these sets. Checking the first few terms of the
, and the same number of isogeny classes of
elliptic curves, and the theory tells us that there is a bijection
between these sets. Checking the first few terms of the ![]() -series
(i.e., comparing the Hecke eigenforms of the newforms with the traces
of Frobenius for the curves) allows us to pair up each isogeny class
with a newform.
-series
(i.e., comparing the Hecke eigenforms of the newforms with the traces
of Frobenius for the curves) allows us to pair up each isogeny class
with a newform.
We will assume that one of the ![]() , which we always label
, which we always label ![]() , is
such that
, is
such that ![]() and
and ![]() (the period lattice of
(the period lattice of ![]() )
are approximately equal. This is true in practice, because our method
of finding the curves in the isogeny class is to compute the
coefficients of a curve from numerical approximations to the
)
are approximately equal. This is true in practice, because our method
of finding the curves in the isogeny class is to compute the
coefficients of a curve from numerical approximations to the ![]() and
and
![]() invariants of
invariants of
![]() ; in all cases these are very close
to integers which are the invariants of the minimal model of an
elliptic curve of conductor
; in all cases these are very close
to integers which are the invariants of the minimal model of an
elliptic curve of conductor ![]() , which we call
, which we call ![]() . The other
curves in the isogeny class are then computed from
. The other
curves in the isogeny class are then computed from ![]() . For the
algorithm described here, however, it is irrelevant how the curves
. For the
algorithm described here, however, it is irrelevant how the curves
![]() were obtained, provided that
were obtained, provided that ![]() and
and ![]() are
close (in a precise sense defined below).
are
close (in a precise sense defined below).
Normalisation of lattices: every lattice ![]() in
in ![]() which
defined over
which
defined over ![]() has a unique
has a unique ![]() -basis
-basis ![]() ,
, ![]() satisfying one of the following:
satisfying one of the following:
For ![]() we know the type from modular symbol calculations, and
we know
we know the type from modular symbol calculations, and
we know
![]() to a certain precision by numerical
integration; modular symbols provide us with cycles
to a certain precision by numerical
integration; modular symbols provide us with cycles
![]() such that the integral of
such that the integral of
![]() over
over
![]() give
give
![]() .
.
For each curve ![]() we compute (to a specific precision) a
we compute (to a specific precision) a ![]() -basis
for its period lattice
-basis
for its period lattice ![]() using the standard AGM method.
Here,
using the standard AGM method.
Here, ![]() is the lattice of periods of the Néron
differential on
is the lattice of periods of the Néron
differential on ![]() . The type of
. The type of ![]() is determined by the
sign of the discriminant of
is determined by the
sign of the discriminant of ![]() : type
: type ![]() for negative discriminant,
and type
for negative discriminant,
and type ![]() for positive discriminant.
for positive discriminant.
For our algorithm we will need to know that ![]() and
and
![]() are approximately equal. To be precise, we know that they
have the same type, and also we verify, for a specific postive
are approximately equal. To be precise, we know that they
have the same type, and also we verify, for a specific postive
![]() , that
, that
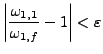 and
and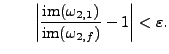
Here
Pulling back the Néron differential on ![]() to
to ![]() gives
gives
![]() where
where
![]() is the Manin constant
for
is the Manin constant
for ![]() . Hence
. Hence
Our task is now to
Our main result is that ![]() and
and ![]() , provided that the precision
bound
, provided that the precision
bound
![]() in (*) is sufficiently small (in most cases,
in (*) is sufficiently small (in most cases,
![]() suffices). In order to state this precisely, we need
some further definitions.
suffices). In order to state this precisely, we need
some further definitions.
A result of Stevens says that in the isogeny class there is a curve,
say ![]() , whose period lattice
, whose period lattice
![]() is contained in
every
is contained in
every ![]() ; this is the unique curve in the class with minimal
Faltings height. (It is conjectured that
; this is the unique curve in the class with minimal
Faltings height. (It is conjectured that ![]() is the
is the
![]() -optimal curve, but we do not need or use this fact. In
many cases, the
-optimal curve, but we do not need or use this fact. In
many cases, the
![]() - and
- and
![]() -optimal curves are
the same, so we expect that
-optimal curves are
the same, so we expect that ![]() often; indeed, this holds for
the vast majority of cases.)
often; indeed, this holds for
the vast majority of cases.)
For each ![]() , we know therefore that
, we know therefore that
![]() and also
and also
![]() . Let
. Let ![]() be the
maximum of
be the
maximum of ![]() and
and ![]() .
.
Firstly,
Then
Hence
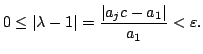
If
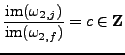
and again we can conclude that
Thus
![]() , from which the result follows.
, from which the result follows.
![]()
Finally, we give a slightly weaker result for
![]() ; in
this range we do not know
; in
this range we do not know ![]() precisely, but only its
projection onto the real line. (The reason for this is that we can
find the newforms using modular symbols for
precisely, but only its
projection onto the real line. (The reason for this is that we can
find the newforms using modular symbols for
![]() ,
which has half the dimension of
,
which has half the dimension of
![]() ; but to find the
exact period lattice requires working in
; but to find the
exact period lattice requires working in
![]() .) The
argument is similar to the one given above, using
.) The
argument is similar to the one given above, using ![]() .
.
First assume that ![]() .
.
If the type of ![]() is the same as that of
is the same as that of ![]() (for
example, this must be the case if all the
(for
example, this must be the case if all the ![]() have the same
type, which will hold whenever all the isogenies between the
have the same
type, which will hold whenever all the isogenies between the ![]() have odd degree) then from
have odd degree) then from
![]() we deduce as before
that
we deduce as before
that ![]() exactly, and
exactly, and
![]() , hence
, hence ![]() . So
in this case we have that
. So
in this case we have that ![]() , though there might be some ambiguity
in which curve is optimal if
, though there might be some ambiguity
in which curve is optimal if ![]() for more than one value of
for more than one value of ![]() .
.
Assume next that ![]() has type
has type ![]() but
but ![]() has type
has type
![]() . Now
. Now
![]() . The usual argument
now gives
. The usual argument
now gives ![]() . Hence either
. Hence either ![]() and
and ![]() , or
, or ![]() and
and
![]() . To see if the latter case could occur, we look for classes
in which
. To see if the latter case could occur, we look for classes
in which ![]() and
and ![]() has type
has type ![]() , while for some
, while for some ![]() we
also have
we
also have ![]() and
and ![]() of type
of type ![]() . This occurs 28 times
for
. This occurs 28 times
for
![]() , but for 15 of these the level
, but for 15 of these the level ![]() is odd, so we
know that
is odd, so we
know that ![]() must be odd. The remaining 13 cases are
must be odd. The remaining 13 cases are
Next suppose that ![]() has type
has type ![]() but
but ![]() has type
has type
![]() . Now
. Now
![]() . The usual argument
now gives
. The usual argument
now gives ![]() , which is impossible; so this case cannot occur.
, which is impossible; so this case cannot occur.
Finally we consider the cases where ![]() . There are only three of
these for
. There are only three of
these for
![]() : namely,
: namely, ![]() ,
, ![]() and
and ![]() ,
where
,
where ![]() . In each case the
. In each case the ![]() all have the same type
(they are linked via
all have the same type
(they are linked via ![]() -isogenies) and the usual argument shows that
-isogenies) and the usual argument shows that
![]() . But none of these levels is divisible by
. But none of these levels is divisible by ![]() , so
, so ![]() in
each case.
in
each case.
![]()
William Stein 2006-06-25