Next: Extensions of Normalized Valuations Up: Extensions and Normalizations of Previous: Extensions and Normalizations of Contents Index
Suppose
![]() is a finite extension of fields, and that
is a finite extension of fields, and that
![]() and
and
![]() are valuations on
are valuations on ![]() and
and ![]() , respectively.
, respectively.
Uniqueness. View ![]() as a
finite-dimensional vector space over
as a
finite-dimensional vector space over ![]() . Then
. Then
![]() is a norm in
the sense defined earlier (Definition 18.1.1). Hence any two
extensions
is a norm in
the sense defined earlier (Definition 18.1.1). Hence any two
extensions
![]() and
and
![]() of
of
![]() are equivalent
as norms, so induce the same topology on
are equivalent
as norms, so induce the same topology on ![]() . But as we have
seen (Proposition 16.1.4), two valuations which induce the same topology are
equivalent valuations, i.e.,
. But as we have
seen (Proposition 16.1.4), two valuations which induce the same topology are
equivalent valuations, i.e.,
![]() , for some
positive real
, for some
positive real ![]() . Finally
. Finally ![]() since
since
![]() for all
for all ![]() .
.
Existence. We do not give a proof of
existence in the general case. Instead we give a proof, which was
suggested by Dr. Geyer at the conference out of which
[Cas67] arose. It is valid when ![]() is locally
compact, which is the only case we will use later.
is locally
compact, which is the only case we will use later.
We see at once that the function defined in (19.1.1)
satisfies the condition (i) that
![]() with equality only
for
with equality only
for ![]() , and (ii)
, and (ii)
![]() for all
for all ![]() . The difficult part of the proof is to show that there is a
constant
. The difficult part of the proof is to show that there is a
constant ![]() such that
such that
Choose a basis
![]() for
for ![]() over
over ![]() . Let
. Let
![]() be the max norm on
be the max norm on ![]() , so for
, so for
![]() with
with ![]() we have
we have

With respect to the
![]() -topology,
-topology, ![]() has the product topology
as a product of copies of
has the product topology
as a product of copies of ![]() . The
function
. The
function
![]() is a composition of continuous functions on
is a composition of continuous functions on ![]() with respect to this topology (e.g.,
with respect to this topology (e.g.,
![]() is the determinant, hence
polynomial),
hence
is the determinant, hence
polynomial),
hence
![]() defines nonzero continuous function on the compact set
defines nonzero continuous function on the compact set
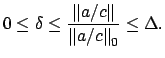
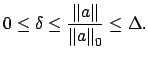
> K<a> := NumberField(x^2-2); > K; Number Field with defining polynomial x^2 - 2 over the Rational Field > function norm(x) return Sqrt(2^(-Valuation(Norm(x),2))); end function; > norm(1+a); 1.0000000000000000000000000000 > norm(1+a+1); 0.70710678118654752440084436209 > z := 3+2*a; > norm(z); 1.0000000000000000000000000000 > norm(z+1); 0.353553390593273762200422181049
 |
||
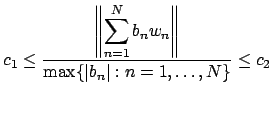
I don't believe this
proof, which I copied from Cassels's article. My problem with it is
that the proof of Theorem 19.1.2 does not give that
![]() , i.e., that the triangle inequality holds for
, i.e., that the triangle inequality holds for
![]() . By
changing the basis for
. By
changing the basis for ![]() one can make any nonzero vector
one can make any nonzero vector ![]() have
have
![]() , so if we choose
, so if we choose ![]() such that
such that
![]() is very large,
then the
is very large,
then the ![]() in the proof will also be very large. One way to fix
the corollary is to only claim that there are positive
constants
in the proof will also be very large. One way to fix
the corollary is to only claim that there are positive
constants
![]() such that
such that
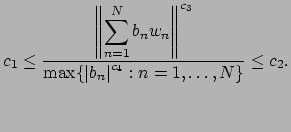
When ![]() is no longer complete under
is no longer complete under
![]() the position is more complicated:
the position is more complicated:
It remains to show that the
![]() are distinct and that they
are the only extensions of
are distinct and that they
are the only extensions of
![]() to
to ![]() .
.
Suppose
![]() is any valuation of
is any valuation of ![]() that extends
that extends
![]() . Then
. Then
![]() extends by continuity to a real-valued function on
extends by continuity to a real-valued function on
![]() ,
which we also denote by
,
which we also denote by
![]() . (We are again using that
. (We are again using that ![]() is dense
in
is dense
in
![]() .) By continuity we have for all
.) By continuity we have for all
![]() ,
,
We consider the restriction of
![]() to one of the
to one of the ![]() . If
. If
![]() for some
for some ![]() , then
, then
![]() for every
for every
![]() in
in ![]() so
so
![]() . Hence either
. Hence either
![]() is identically
0 on
is identically
0 on ![]() or it induces a valuation on
or it induces a valuation on ![]() .
.
Further,
![]() cannot induce a valuation on two of the
cannot induce a valuation on two of the ![]() . For
. For
It remains only to show that (19.1.2) is a topological homomorphism. For
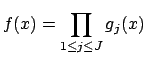
William Stein 2004-05-06