The Exact Sequence

There is a natural reduction homomorphism

$$\varphi :D_\mathfrak{p}\to {\mathrm{Gal}}(\mathbf{F}_\mathfrak{p}/\mathbf{F}_p).$$

Theorem 14.1.5   The homomorphism $\varphi$ is surjective.

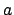
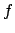
Proof. Let $\tilde{a} \in \mathbf{F}_\mathfrak{p}$ be an element such that $\mathbf{F}_\mathfrak{p}=\mathbf{F}_p(a)$. Lift $\tilde{a}$ to an algebraic integer $a\in\O _K$, and let $f=\prod_{\sigma\in D_p}(x-\sigma(a))\in K^D[x]$ be the characteristic polynomial of $a$ over $K^D$. Using Proposition 14.1.4 we see that $f$ reduces to the minimal polynomial $\tilde{f}=\prod (x-\tilde{\sigma(a)})\in \mathbf{F}_p[x]$ of $\tilde{a}$ (by the Proposition the coefficients of $\tilde{f}$ are in $\mathbf{F}_p$, and $\tilde{a}$ satisfies $\tilde{f}$, and the degree of $\tilde{f}$ equals the degree of the minimal polynomial of $\tilde{a}$). The roots of $\tilde{f}$ are of the form $\tilde{\sigma}(a)$, and the element $\Frob _p(a)$ is also a root of $\tilde{f}$, so it is of the form $\tilde{\sigma(a)}$. 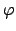We conclude that the generator $\Frob _p$ of ${\mathrm{Gal}}(\mathbf{F}_\mathfrak{p}/\mathbf{F}_p)$ is in the image of $\varphi$, which proves the theorem. $\qedsymbol$

Definition 14.1.6 (Inertia Group)   The is the kernel $I_\mathfrak{p}$ of $D_\mathfrak{p}\to{\mathrm{Gal}}(\mathbf{F}_\mathfrak{p}/\mathbf{F}_p)$.

Combining everything so far, we find an exact sequence of groups

$$1 \to I_\mathfrak{p}\to D_\mathfrak{p}\to {\mathrm{Gal}}(\mathbf{F}_\mathfrak{p}/\mathbf{F}_p)\to 1.$$ (14.1)

The inertia group is a measure of how $p$ ramifies in $K$.

Corollary 14.1.7   We have $\char93 I_\mathfrak{p}= e(\mathfrak{p}/p)$, where $\mathfrak{p}$ is a prime of $K$ over $p$.

Proof. The sequence (14.1.1) implies that $\char93 I_\mathfrak{p}= \char93 D_\mathfrak{p}/f(K/\mathbf{Q})$. Applying Propositions 14.1.3-14.1.4, we have

$$\char93 D_\mathfrak{p}= [K:L] = \frac{[K:\mathbf{Q}]}{g} = \frac{efg}{g} = ef.$$

Dividing both sides by $f=f(K/\mathbf{Q})$ proves the corollary. $\qedsymbol$

We have the following characterization of $I_\mathfrak{p}$.

Proposition 14.1.8   Let $K/\mathbf{Q}$ be a Galois extension with group $G$, let $\mathfrak{p}$ be a prime lying over a prime $p$. Then

$$I_\mathfrak{p}= \{\sigma\in G : \sigma(a) = a\pmod{\mathfrak{p}}$$ for all $$a\in\O _K\}.$$

Proof. By definition $I_\mathfrak{p}= \{\sigma\in D_\mathfrak{p}: \sigma(a) = a\pmod{\mathfrak{p}}$ for all $a\in\O _K\}$, so it suffices to show that if $\sigma\not\in D_\mathfrak{p}$, then there exists $a\in\O _K$ such that $\sigma(a)=a\pmod{\mathfrak{p}}$. 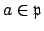If $\sigma\not\in D_\mathfrak{p}$, we have $\sigma^{-1}(\mathfrak{p})\neq \mathfrak{p}$, so since both are maximal ideals, there exists $a\in\mathfrak{p}$ with $a\not\in\sigma^{-1}(\mathfrak{p})$, i.e., $\sigma(a)\not\in\mathfrak{p}$. Thus $\sigma(a)\not\equiv a\pmod{\mathfrak{p}}$. $\qedsymbol$

Figure 14.1.2 is a picture of the splitting behavior of a prime $p\in\mathbf{Z}$.

Figure 14.1.1: The Splitting of Behavior of a Prime in a Galois Extension