Next: Norms of Ideals Up: Discrimannts, Norms, and Finiteness Previous: Preliminary Remarks Contents Index
If we consider
![]() instead, we
obtain a number that is a well-defined integer which can
be either positive or negative. Note that
instead, we
obtain a number that is a well-defined integer which can
be either positive or negative. Note that
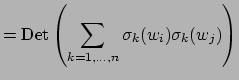 |
||
If we view ![]() as a
as a
![]() -vector space, then
-vector space, then
![]() defines a bilinear pairing
defines a bilinear pairing
![]() on
on ![]() , which we call
the . The following lemma asserts that this
pairing is nondegenerate, so
, which we call
the . The following lemma asserts that this
pairing is nondegenerate, so
![]() hence
hence
![]() .
.
Warning: In ![]() is defined to be the discriminant of the
polynomial you happened to use to define
is defined to be the discriminant of the
polynomial you happened to use to define ![]() , which is (in my opinion)
a poor choice and goes against most of the literature.
, which is (in my opinion)
a poor choice and goes against most of the literature.
The following proposition asserts that the discriminant of an order
![]() in
in ![]() is bigger than
is bigger than
![]() by a factor of the square
of the index.
by a factor of the square
of the index.
This result is enough to give an algorithm for computing ![]() ,
albeit a potentially slow one. Given
,
albeit a potentially slow one. Given ![]() , find some order
, find some order
![]() , and compute
, and compute
![]() . Factor
. Factor ![]() , and use the factorization
to write
, and use the factorization
to write
![]() , where
, where ![]() is the largest square that
divides
is the largest square that
divides ![]() . Then the index of
. Then the index of ![]() in
in ![]() is a divisor of
is a divisor of ![]() ,
and we (tediously) can enumerate all rings
,
and we (tediously) can enumerate all rings ![]() with
with
![]() and
and
![]() , until we find the largest one all of
whose elements are integral.
, until we find the largest one all of
whose elements are integral.
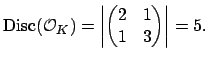
![$\displaystyle \Disc (\O ) = \left\vert \left(
\begin{matrix}2&0\ 0&10
\end{matrix}\right) \right\vert = 20 = [\O _K:\O ]^2\cdot 5.
$](img764.png)
William Stein 2004-05-06