An order in a number field 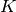 is a subring of
is a subring of 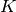 whose
rank over
whose
rank over  equals the degree of
equals the degree of 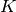 . For
example, if
. For
example, if 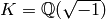 , then
, then
![\mathbb{Z}[7i]](_images/math/aee4fd11b0ee1e04e3e188e2ce2ca459063b6668.png) is an order in
is an order in 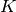 . A good first exercise
is to prove that every element of an order is an algebraic integer.
. A good first exercise
is to prove that every element of an order is an algebraic integer.
sage: K.<I> = NumberField(x^2 + 1)
sage: R = K.order(7*I)
sage: R
Order in Number Field in I with defining polynomial x^2 + 1
sage: R.basis()
[1, 7*I]
Using the discriminant command, we compute the discriminant of this order:
sage: factor(R.discriminant())
-1 * 2^2 * 7^2
You can give any list of elements of the number field, and it will
generate the smallest ring 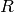 that contains them.
that contains them.
sage: K.<a> = NumberField(x^4 + 2)
sage: K.order([12*a^2, 4*a + 12]).basis()
[1, 4*a, 4*a^2, 16*a^3]
If 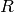 isn’t of rank equal to the degree of the number
field (i.e.,
isn’t of rank equal to the degree of the number
field (i.e., 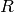 isn’t an order), then you’ll get an error
message.
isn’t an order), then you’ll get an error
message.
sage: K.order([a^2])
...
ValueError: the rank of the span of gens is wrong
We can also compute the maximal order, using the maxima order
command, which behind the scenes finds an integral basis using Pari’s
nfbasis command. For example, ![\mathbb{Q}(\sqrt[4]{2})](_images/math/a43550110d27a999ba4c49492f765164e58ad7f9.png) has
maximal order
has
maximal order ![\mathbb{Z}[\sqrt[4]{2}]](_images/math/c649d26a549e83cca1e6b766c7f7e589bd7347f4.png) , and if
, and if  is a root of
is a root of 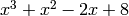 , then
, then 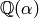 has maximal order with
has maximal order with  -basis
-basis
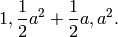
sage: K.<a> = NumberField(x^4 + 2)
sage: K.maximal_order().basis()
[1, a, a^2, a^3]
sage: L.<a> = NumberField(x^3 + x^2 - 2*x+8)
sage: L.maximal_order().basis()
[1, 1/2*a^2 + 1/2*a, a^2]
sage: L.maximal_order().basis()[1].minpoly()
x^3 - 2*x^2 + 3*x - 10
There is still much important functionality for computing with non-maximal orders that is missing in Sage. For example, there is no support at all in Sage for computing with modules over orders or with ideals in non-maximal orders.
sage: K.<a> = NumberField(x^3 + 2)
sage: R = K.order(3*a)
sage: R.ideal(5)
...
NotImplementedError: ideals of non-maximal orders not
yet supported.
A relative number field  is a number field of the form
is a number field of the form
 , where
, where 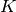 is a number field, and an absolute
number field is a number field presented in the form
is a number field, and an absolute
number field is a number field presented in the form
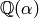 . By the primitive element theorem, any
relative number field
. By the primitive element theorem, any
relative number field  can be written as
can be written as
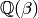 for some
for some 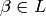 . However, in
practice it is often convenient to view
. However, in
practice it is often convenient to view  as
as
 . In Symbolic Expressions, we constructed the
number field
. In Symbolic Expressions, we constructed the
number field 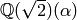 , where
, where
 is a root of
is a root of 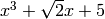 , but not as
a relative field–we obtained just the number field defined by a root
of
, but not as
a relative field–we obtained just the number field defined by a root
of  .
.
To construct this number field as a relative number field, first we
let 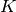 be
be 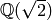 .
.
sage: K.<sqrt2> = QuadraticField(2)
Next we create the univariate polynomial ring ![R = K[X]](_images/math/3727226b29f829d024e4ffc07999fac63742d297.png) . In
Sage, we do this by typing R.<X> = K[]. Here R.<X> means
“create the object
. In
Sage, we do this by typing R.<X> = K[]. Here R.<X> means
“create the object 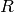 with generator
with generator 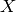 ” and K[]
means a “polynomial ring over
” and K[]
means a “polynomial ring over 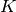 “, where the generator is named
based on the afformentioned
“, where the generator is named
based on the afformentioned 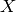 (to create a polynomial ring in
two variables
(to create a polynomial ring in
two variables 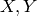 simply replace R.<X> by R.<X,Y>).
simply replace R.<X> by R.<X,Y>).
sage: R.<X> = K[]
sage: R
Univariate Polynomial Ring in X over Number Field in sqrt2
with defining polynomial x^2 - 2
Now we can make a polynomial over the number field
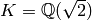 , and construct the extension of
, and construct the extension of
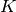 obtained by adjoining a root of that polynomial to
obtained by adjoining a root of that polynomial to
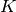 .
.
sage: L.<a> = K.extension(X^3 + sqrt2*X + 5)
sage: L
Number Field in a with defining polynomial X^3 + sqrt2*X + 5...
Finally,  is the number field
is the number field
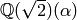 , where
, where  is a root
of
is a root
of 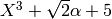 . We can do now do arithmetic in
this number field, and of course include
. We can do now do arithmetic in
this number field, and of course include  in
expressions.
in
expressions.
sage: a^3
(-sqrt2)*a - 5
sage: a^3 + sqrt2*a
-5
The relative number field  also has numerous functions, many
of which are by default relative. For example the degree function
on
also has numerous functions, many
of which are by default relative. For example the degree function
on  returns the relative degree of
returns the relative degree of  over
over 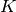 ;
for the degree of
;
for the degree of  over
over  use the
absolute_degree function.
use the
absolute_degree function.
sage: L.degree()
3
sage: L.absolute_degree()
6
Given any relative number field you can also an absolute number field
that is isomorphic to it. Below we create 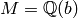 ,
which is isomorphic to
,
which is isomorphic to  , but is an absolute field over
, but is an absolute field over
 .
.
sage: M.<b> = L.absolute_field()
sage: M
Number Field in b with defining
polynomial x^6 + 10*x^3 - 2*x^2 + 25
The structure function returns isomorphisms in both directions
between  and
and  .
.
sage: M.structure()
(Isomorphism from Number Field in b ...,
Isomorphism from Number Field in a ...)
In Sage one can create arbitrary towers of relative number fields (unlike in Pari, where a relative extension must be a single extension of an absolute field).
sage: R.<X> = L[]
sage: Z.<b> = L.extension(X^3 - a)
sage: Z
Number Field in b with defining polynomial
X^3 + (-1)*a over its base field
sage: Z.absolute_degree()
18
Note
Exercise: Construct the relative number field
![L = K(\sqrt[3]{\sqrt{2}+\sqrt{3}})](_images/math/32ced835ef6d5fe6aab50b7d3138155b1f494b38.png) , where
, where
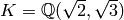 .
.
One shortcoming with relative extensions in Sage is that behind the scenes all arithmetic is done in terms of a single absolute defining polynomial, and in some cases this can be very slow (much slower than Magma). Perhaps this could be fixed by using Singular’s multivariate polynomials modulo an appropriate ideal, since Singular polynomial arithmetic is extremely flast. Also, Sage has very little direct support for constructive class field theory, which is a major motivation for explicit computation with relative orders; it would be good to expose more of Pari’s functionality in this regard.