Modular Abelian Varieties

The quotient of the extended upper half plane 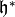by the congruence subgroup 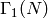is the modular curve 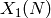. Its Jacobian 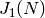is an abelian variety that is canonically defined over . Likewise, one defines a modular abelian variety associated to .

A modular abelian variety is an abelian variety over that is a quotient of for some .

The biggest recent theorem in number theory is the proof of Serre’s conjecture by Khare and Wintenberger. According to an argument of Ribet and Serre, this implies the following modularity theorem, which generalizes the modularity theorem that Taylor-Wiles proved in the course of proving Fermat’s Last Theorem.

One of my longterm research goals is to develop a systematic theory for computing with modular abelian varieties. A good start is the observation using the Abel-Jacobi theorem that every modular abelian variety (up to isomorphism) can be specified by giving a lattice in a space of modular symbols.

Computing in Sage

We define some modular abelian varieties of level , and compute some basic invariants.

sage: D = J0(39).decomposition(); D
[
Simple abelian subvariety 39a(1,39) of dimension 1 of J0(39),
Simple abelian subvariety 39b(1,39) of dimension 2 of J0(39)
]
sage: D[1].lattice()
Free module of degree 6 and rank 4 over Integer Ring
Echelon basis matrix:
[ 1  0  0  1 -1  0]
[ 0  1  1  0 -1  0]
[ 0  0  2  0 -1  0]
[ 0  0  0  0  0  1]
sage: G = D[1].rational_torsion_subgroup(); G
Torsion subgroup of Simple abelian subvariety 39b(1,39)
of dimension 2 of J0(39)
sage: G.order()
28
sage: G.gens()
[[(1/14, 2/7, 0, 1/14, -3/14, 1/7)], [(0, 1, 0, 0, -1/2, 0)],
 [(0, 0, 1, 0, -1/2, 0)]]
sage: B, phi = D[1]/G
sage: B
Abelian variety factor of dimension 2 of J0(39)
sage: phi.kernel()
(Finite subgroup with invariants [2, 14] ...

Endomorphisms

There is an algorithm in Sage for computing the exact endomorphism ring of any modular abelian variety.

sage: A = J0(91)[2]; A
Simple abelian subvariety 91c(1,91) of dimension 2 of J0(91)
sage: R = End(A); R
Endomorphism ring of Simple abelian subvariety 91c(1,91)
of dimension 2 of J0(91)
sage: for x in R.gens(): print x.matrix(),'\n'
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]

[ 0  4 -2  0]
[-1  5 -2  1]
[-1  2  0  2]
[-1  1  0  3]

It is also possible to test isomorphism of two modular abelian varieties. But much exciting theoretical and computational work remains to be done.