



Next: Non-liftable weight one modular
Up: Modular Forms Modulo
Previous: Modular Forms Modulo
Contents
This section was written by Gabor Wiese.
To every mod 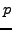 eigenform Deligne attaches a 2-dimensional odd "mod
eigenform Deligne attaches a 2-dimensional odd "mod
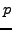 " Galois representation, i.e. a continuous group homomorphism
" Galois representation, i.e. a continuous group homomorphism
The trace of a Frobenius element at a prime 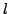 is for almost all
is for almost all 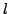 given by the
given by the 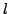 -th coefficient of the (normalised) eigenform. By
continuity, the image of such a representation is a finite group.
-th coefficient of the (normalised) eigenform. By
continuity, the image of such a representation is a finite group.
Problem 2.1.1
Find group theoretic criteria that allow one (in some cases) to
determine the image computationally.
Remark 2.1.2 (From Richard Taylor)
Problem
2.1.1 seems to me straightforward.
(Richard, Grigor, and Stein did something like this for
elliptic curves over
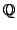
-- see
http://modular.math.washington.edu/papers/bsdalg/.)
Problem 2.1.3
Implement in
SAGE the algorithm of Problem
2.1.1.
Problem 2.1.4
Carry out systematic computations of mod
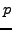
modular forms in order to
find ``big'' images.
Like this one can certainly realise some groups as Galois groups over
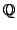 that were not known to occur before!
that were not known to occur before!




Next: Non-liftable weight one modular
Up: Modular Forms Modulo
Previous: Modular Forms Modulo
Contents
William Stein
2006-10-20
![]() eigenform Deligne attaches a 2-dimensional odd "mod
eigenform Deligne attaches a 2-dimensional odd "mod
![]() " Galois representation, i.e. a continuous group homomorphism
" Galois representation, i.e. a continuous group homomorphism
![]() that were not known to occur before!
that were not known to occur before!