



Next: Higher Level
Up: Characteristic Polynomials of Hecke
Previous: Characteristic Polynomials of Hecke
Contents
Level 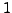 Weight
Weight 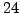
Gather data and theoretical results about the following question,
which Ralph Greenberg asked (though surely other people have
asked it):
Problem 1.1.1
Is the characteristic polynomial of
every Hecke operator
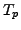
irreducible on the 2-dimensional space of cusp forms of level 1 and
weight 24? (Stein checked that it is for all primes up to 800 and
for p=144169.)
The rest of this section was written by Koopa Koo, and explains
some results related to (1.1.1).
The goal of this section is to explain how to apply Chebotarev's density
theorem to obtain density result about irreducibility of the
characteristic polynomial of the Hecke operators attached to the
weight 24 cusp forms of level 1,
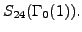
I would like to thank my advisor
Prof. Ralph Greenberg for suggesting the problem with helpful
suggestions, Prof. Gabor Wiese for his helpful suggestions, and my
greatest thanks to Prof. William Stein, who advised the project and
provided many inspiring ideas.


Problem 1.1.2
I expect the same method generalizes to higher weight and higher
level, by working with mod
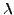
representations. Help me carry
out this generalization and write up the details nicely.




Next: Higher Level
Up: Characteristic Polynomials of Hecke
Previous: Characteristic Polynomials of Hecke
Contents
William Stein
2006-10-20
![]()

