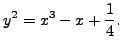
Let
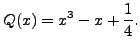
In our case, we compute
as
in
and compute the appropriate list of differentials:
|
|
||
| 0 |
|
|
| 1 |
|
|
| 2 |
|
|
| 0 |
|
|
| 1 |
|
|
| 2 |
|
Thus we wish to write
![]() as a linear combination of
as a linear combination of
![]() ,
,
![]() , and
, and
![]() , all
modulo 25 (we may ignore the lower powers of
, all
modulo 25 (we may ignore the lower powers of ![]() present in the
differentials, as we will take care of them in the steps to come).
We find that taking
present in the
differentials, as we will take care of them in the steps to come).
We find that taking
leaves us with
Now we wish to write
![]() as a linear combination of
as a linear combination of
![]() ,
,
![]() , and
, and
![]() ,
modulo 25. We find that taking
,
modulo 25. We find that taking
leaves us with
Next, we reduce
Note that this has an
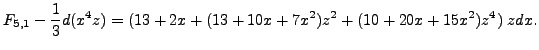
Now we proceed as in the case of ![]() , and we wish to write
, and we wish to write
![]() as a linear combination of
as a linear combination of
![]() ,
,
![]() , and
, and
![]() , all modulo
25. We find that taking
, all modulo
25. We find that taking
leaves us with
Finally, we wish to write
![]() as a linear
combination of
as a linear
combination of
![]() ,
,
![]() , and
, and
![]() , all modulo 25. We find that taking
, all modulo 25. We find that taking
leaves us with
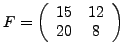 .
.