



Next: Half Integral Weight Modular
Up: Computing with Classical Modular
Previous: Weight
Contents
This section was written by Ralph Greenberg.
Definition 4.4.1 (Irregular Prime)
A prime
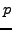
is said to be
irregular if
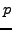
divides the numerator of a
Bernoulli number
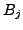
, where
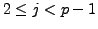
and
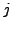
is even.
(For odd
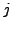
, one has
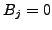
.)
The index of irregularity for a prime 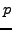 is the number of such
is the number of such
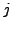 .'s There is considerable numerical data concerning the statistics
of irregular primes - the proportion of
.'s There is considerable numerical data concerning the statistics
of irregular primes - the proportion of 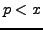 which are irregular or
which have a certain index of irregularity. (See Irregular
primes and cyclotomic invariants to four million, Buhler et al., in
Math. of Comp., vol. 61, (1993), 151-153.)
which are irregular or
which have a certain index of irregularity. (See Irregular
primes and cyclotomic invariants to four million, Buhler et al., in
Math. of Comp., vol. 61, (1993), 151-153.)
Let
for each 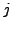 as above. According to the Kummer congruences,
as above. According to the Kummer congruences, 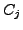 is a
is a
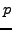 -integer, i.e., its denominator is not divisible by
-integer, i.e., its denominator is not divisible by 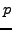 . But its
numerator could be divisible by
. But its
numerator could be divisible by 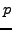 . This happens for
. This happens for 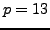 and
and 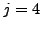 .
.
Problem 4.4.2
Obtain numerical data for the divisibility of
the numerator of
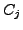
by a prime
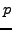
analogous to that for the
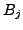
's.
Motivation: It would be interesting to find an example of a prime 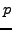 and an index
and an index 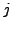 (with
(with
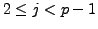 ,
, 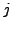 even) such that
even) such that 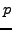 divides the numerator of both
divides the numerator of both 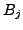 and
and 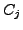 . Then the
. Then the 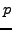 -adic
-adic
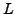 -function for a certain even character of conductor
-function for a certain even character of conductor 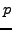 (namely,
the
(namely,
the 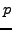 -adic valued character
-adic valued character 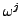 , where
, where 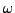 is the
character characterized by
is the
character characterized by
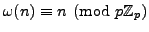 for
for
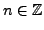 ) would have at least two zeros. No such example exists for
) would have at least two zeros. No such example exists for
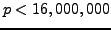 . The
. The 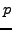 -adic
-adic 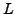 -functions for those primes have at
most one zero. If the statistics for the
-functions for those primes have at
most one zero. If the statistics for the 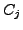 's are similar to those
for the
's are similar to those
for the 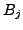 's, then a probabilistic argument would suggest that
examples should exist.
's, then a probabilistic argument would suggest that
examples should exist.
Problem 4.4.3
Computation of
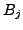
for a specific
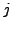
is very efficient in PARI,
hence in
SAGE via the command
bernoulli. Methods for
computation of
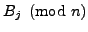
for a large range of
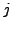
are described
in
Irregular primes and cyclotomic invariants to four million,
Buhler et al. Implement the method of Buhler et al. in
SAGE.




Next: Half Integral Weight Modular
Up: Computing with Classical Modular
Previous: Weight
Contents
William Stein
2006-10-20
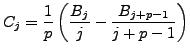
![]() and an index
and an index ![]() (with
(with
![]() ,
, ![]() even) such that
even) such that ![]() divides the numerator of both
divides the numerator of both ![]() and
and ![]() . Then the
. Then the ![]() -adic
-adic
![]() -function for a certain even character of conductor
-function for a certain even character of conductor ![]() (namely,
the
(namely,
the ![]() -adic valued character
-adic valued character ![]() , where
, where ![]() is the
character characterized by
is the
character characterized by
![]() for
for
![]() ) would have at least two zeros. No such example exists for
) would have at least two zeros. No such example exists for
![]() . The
. The ![]() -adic
-adic ![]() -functions for those primes have at
most one zero. If the statistics for the
-functions for those primes have at
most one zero. If the statistics for the ![]() 's are similar to those
for the
's are similar to those
for the ![]() 's, then a probabilistic argument would suggest that
examples should exist.
's, then a probabilistic argument would suggest that
examples should exist.