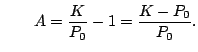The logistics equation is a differential equation that models
population growth. Often in practice a differential equation models
some physical situtation, and you should ``read it'' as doing so.
Exponential growth:
This says that the ``relative (percentage) growth rate'' is constant.
As we saw before, the solutions are
Note that this model only works for a little while. In everyday life
the growth couldn't actually continue at this rate indefinitely. This
exponential growth model ignores limitations on resources, disease,
etc. Perhaps there is a better model?
Over time we expect the growth rate should level off, i.e., decrease
to 0.
What about
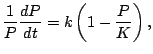 |
(7.1) |
where 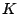 is some large constant called the carrying capacity,
which is much bigger than
is some large constant called the carrying capacity,
which is much bigger than 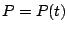 at time 0. The carrying capacity
is the maximum population that the environment can support.
Note that if
at time 0. The carrying capacity
is the maximum population that the environment can support.
Note that if 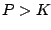 , then
, then 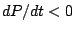 so the population declines.
The differential equation (
so the population declines.
The differential equation (![[*]](/usr/share/latex2html/icons/crossref.png) ) is called the logistic
model (or logistic differential equation). There are, of course,
other models one could use, e.g., the Gompertz equation.
) is called the logistic
model (or logistic differential equation). There are, of course,
other models one could use, e.g., the Gompertz equation.
First question: are there any equilibrium solutions to
(![[*]](/usr/share/latex2html/icons/crossref.png) ), i.e., solutions with
), i.e., solutions with 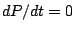 , i.e., constant
solutions? In order that
, i.e., constant
solutions? In order that 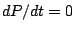 then
then
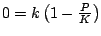 , so the two equilibrium solutions are
, so the two equilibrium solutions are 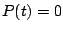 and
and
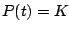 .
.
The logistic differential equation (![[*]](/usr/share/latex2html/icons/crossref.png) ) is separable,
so you can separate the variables with one variable on one side of
the equality and one on the other. This means we can easily solve
the equation by integrating. We rewrite the equation as
) is separable,
so you can separate the variables with one variable on one side of
the equality and one on the other. This means we can easily solve
the equation by integrating. We rewrite the equation as
Now separate:
and integrate both sides
On the left side we get
Thus
so
Now exponentiate both sides:
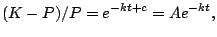
where $A=e^c$

Thus
so
Note that 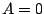 also makes sense and gives an equilibrium solution.
In general we have
also makes sense and gives an equilibrium solution.
In general we have
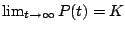 .
In any particular case we can determine
.
In any particular case we can determine 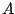 as a function of
as a function of
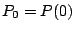 by using that
by using that
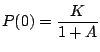
so
William Stein
2006-03-15
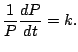
![]() ), i.e., solutions with
), i.e., solutions with ![]() , i.e., constant
solutions? In order that
, i.e., constant
solutions? In order that ![]() then
then
![]() , so the two equilibrium solutions are
, so the two equilibrium solutions are ![]() and
and
![]() .
.
![]() ) is separable,
so you can separate the variables with one variable on one side of
the equality and one on the other. This means we can easily solve
the equation by integrating. We rewrite the equation as
) is separable,
so you can separate the variables with one variable on one side of
the equality and one on the other. This means we can easily solve
the equation by integrating. We rewrite the equation as
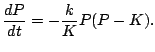
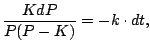
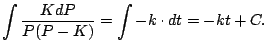
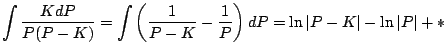
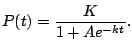
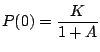 so
so