Next: Convergence of Power Series Up: Power Series Previous: Power Series Contents Index
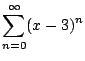 |
||
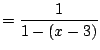 equality valid when equality valid when |
||
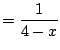 |
Power series can be written in different ways, which have different advantages and disadvantages. For example,
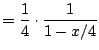 |
||
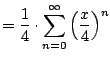 converges for all converges for all |
William Stein 2006-03-15