Next: Trigonometric Substitutions Up: Trigonometric Integrals Previous: Trigonometric Integrals Contents Index
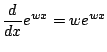
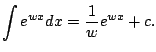
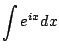 |
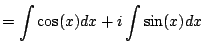 |
|
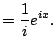 |
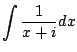 . Wouldn't it be nice if
we could just write
. Wouldn't it be nice if
we could just write
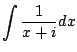 |
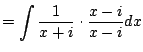 |
|
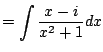 |
||
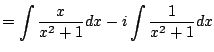 |
||
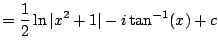 |
The next example illustrates an alternative to the method of Section 5.2.
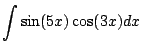 |
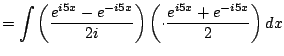 |
|
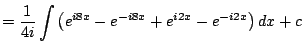 |
||
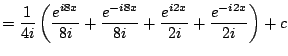 |
||
![$\displaystyle = -\frac{1}{4}\left[\frac{1}{4}\cos(8x) + \cos(2x)\right] + c$](img614.png) |
William Stein 2006-03-15