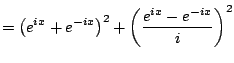Amazingly, trig functions can also be expressed back in terms of the
complex exponential. Then everything involving trig functions
can be transformed into something involving the exponential function.
This is very surprising.
In order to easily obtain trig identities like
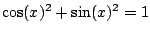 , let's write
, let's write 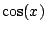 and
and 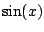 as complex exponentials.
From the definitions we have
as complex exponentials.
From the definitions we have
so
Adding these two equations and dividing by 2 yields
a formula for 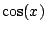 , and subtracting and dividing
by
, and subtracting and dividing
by 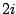 gives a formula for
gives a formula for 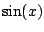 :
:
We can now derive trig identities. For example,
I'm unimpressed, given that you can get this much
more directly using
and equating imaginary parts.
But there are more interesting examples.
Next we verify that (4.4.1) implies
that
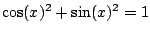 . We have
. We have
The equality just appears as a follow-your-nose algebraic
calculation.
Example 4.4.4
Compute
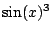
as a sum of sines and
cosines with no powers.
Figure:
What is 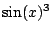 ?
?
|
|
Solution. We use (
4.4.1):
William Stein
2006-03-15
![]() , let's write
, let's write ![]() and
and ![]() as complex exponentials.
From the definitions we have
as complex exponentials.
From the definitions we have
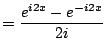
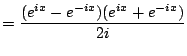
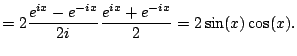
![]() . We have
. We have