Next: Substitution and Symmetry Up: Indefinite Integrals and Change Previous: Examples Contents Index
The following is a restatement of the fundamental theorem of calculus:
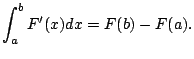
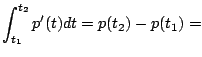 change in number of students from time $t_1$ to $t_2$
change in number of students from time $t_1$ to $t_2$
Another very common example you'll seen in problems involves water
flow into or out of something. If the volume of water in your bathtub
is ![]() gallons at time
gallons at time ![]() (in seconds), then the rate at which
your tub is draining is
(in seconds), then the rate at which
your tub is draining is ![]() gallons per second. If you have the
geekiest drain imaginable, it prints out the drainage rate
gallons per second. If you have the
geekiest drain imaginable, it prints out the drainage rate ![]() .
You can use that printout to determine how much water drained out from
time
.
You can use that printout to determine how much water drained out from
time ![]() to
to ![]() :
:
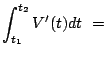
Some problems will try to confuse you with different notions of
change. A standard example is that if a car has velocity
![]() , and you drive forward, then slam it in reverse and drive
backward to where you start (say 10 seconds total elapse), then
, and you drive forward, then slam it in reverse and drive
backward to where you start (say 10 seconds total elapse), then ![]() is positive some of the time and negative some of the time. The
integral
is positive some of the time and negative some of the time. The
integral
![]() is not the total distance registered
on your odometer, since
is not the total distance registered
on your odometer, since ![]() is partly positive and partly negative.
If you want to express how far you actually drove going back and
forth, compute
is partly positive and partly negative.
If you want to express how far you actually drove going back and
forth, compute
![]() . The following example
emphasizes this distinction:
. The following example
emphasizes this distinction:
For (1), we compute
![$\displaystyle \int_{1}^6 (t^2 - 2t - 8) dt = \left[ \frac{1}{3} t^3 - t^2 - 8t \right]_{1}^6 = - \frac{10}{3}.$](img114.png) |
For (2), we compute the integral of ![]() :
:
![$\displaystyle \int_{1}^6 \vert t^2 - 2t - 8\vert dt = \left[ -\left(\frac{1}{3}...
...t[ \frac{1}{3} t^3 - t^2 - 8t \right]_{4}^6 = 18 + \frac{44}{3} = \frac{98}{3}.$](img116.png) |
William Stein 2006-03-15