Next: Examples Up: Indefinite Integrals and Change Previous: Indefinite Integrals and Change Contents Index
We thus often write
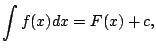
Note that the proposition need not be true if ![]() is not defined
on a whole interval.
For example,
is not defined
on a whole interval.
For example,
![]() is not defined at 0. For any pair
of constants
is not defined at 0. For any pair
of constants ![]() ,
, ![]() , the function
, the function
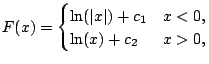
We pause to emphasize the notation difference between definite and indefinite integration.
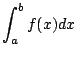 |
||
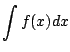 |
One of the main goals of this course is to help you to get
really good at computing
![]() for various functions
for various functions ![]() .
It is useful to memorize a table of examples (see, e.g., page 406 of
Stewart), since often the trick to integration is to relate a given
integral to a known one. Integration is like solving a puzzle or
playing a game, and often you win by moving into a position where you
know how to defeat your opponent, e.g., relating your integral to
integrals that you already know how to do. If you know how to
do a basic collection of integrals, it will be easier for you
to see how to get to a known integral from an unknown one.
.
It is useful to memorize a table of examples (see, e.g., page 406 of
Stewart), since often the trick to integration is to relate a given
integral to a known one. Integration is like solving a puzzle or
playing a game, and often you win by moving into a position where you
know how to defeat your opponent, e.g., relating your integral to
integrals that you already know how to do. If you know how to
do a basic collection of integrals, it will be easier for you
to see how to get to a known integral from an unknown one.
Whenever you successfully compute
![]() , then you've
constructed a mathematical gadget that allows you to very
quickly compute
, then you've
constructed a mathematical gadget that allows you to very
quickly compute
![]() for any
for any ![]() (in the interval of
definition of
(in the interval of
definition of ![]() ). The gadget is
). The gadget is
![]() . This is really
powerful.
. This is really
powerful.
William Stein 2006-03-15